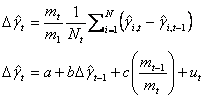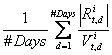Program Report: Asset Pricing, 2005
Introduction
Members of the NBER's Asset Pricing Program produce over 100 working papers in a typical year. These papers are spread over an astonishing range of topic areas. Naming the papers written in the four and a half years since the last program report, let alone providing any sort of intelligible summary of their contents, would quickly fill the available space and exhaust the most dedicated reader's patience. Therefore, I'll describe in depth one area that strikes me as particularly interesting and that may be novel to likely readers of this report. I proceed with an apology to all the authors whose papers are thus omitted. In addition, I confine myself to papers in the NBER Working Paper series or presented at Asset Pricing Program Meetings in the last four and a half years. I apologize in advance to non-NBER authors and to authors of older papers whose work should be discussed in a comprehensive literature review.
My focus here goes by a variety of names, including liquidity, trading, volume, market frictions, short-sales constraints, and limits to arbitrage. For a long time, there has been an implicit separation of effort in asset pricing: Researchers operating in the frictionless macroeconomics-based tradition study the broad level of prices, while researchers in the market microstructure tradition -- filled with non-Walrasian trading, asymmetric information, and so on -- pretty much study small (but interesting) refinements, where prices fall in the bid-ask spread rather than where the spread is in the first place.
Recently, this separation has begun to erode. At one level, this erosion is the beginning of a long-expected understanding of trading and volume. The classic theory of finance has no volume at all: prices adjust until investors are happy to continue doing what they were doing all along, holding the market portfolio. Simple modifications, such as lifecycle and rebalancing motives, don't come near to explaining observed volume. Put bluntly, the classic theory of finance predicts that the NYSE and NASDAQ do not exist. Lifecycle stock trading could be handled at a retail level, like (say) life insurance. The markets exist to support high frequency trading. They are at bottom markets of information (or, some might say, opinion), not really markets for stocks and bonds.
Now, perhaps prices are set as if volume is zero, and then volume and the attendant microstructure issues can be studied separately. But perhaps not; perhaps volume, trading, liquidity, and market structure effects spill over to affect the level of prices. This is the issue I focus on. I start with empirical work, and follow with economic modeling that tries to understand the emerging set of facts.
Empirical Work
3Com, Palm and Convenience Yield
Work by Owen A. Lamont and Richard H. Thaler(2) most vividly brought this constellation of ideas to my attention. They start with the case of 3Com and Palm. On March 2, 2000, 3Com sold 5 percent of Palm in an initial public offering. 3Com retained about 95 percent of the shares, and announced that it would distribute those shares to 3Com shareholders by the end of the year at about 1.5 shares per one 3Com share. Thus, one could obtain 150 Palm shares in two ways: buy 150 Palm shares directly or buy 100 3Com shares and end up in six months with 150 Palm as well as 100 3Com.
Surely the latter strategy should cost more. But in fact, the latter strategy was cheaper. Palm prices exploded, 3Com prices fell, and at the end of the first day of trading the "stub value" of 3Com shares (the value of 3Com less the embedded Palm shares) was negative $63! This violation of the law of one price lasted for quite a while, as shown in Lamont and Thaler's Figure 3. The event was not unique. Lamont and Thaler study six additional cases of persistent negative stub values in a carve-out followed by a spin-off.
Lamont and Thaler carefully document that these events did not present exploitable arbitrage opportunities. Most simply, a trader might want to short Palm and buy 3Com. But the costs of shorting were so high as to make this trade unprofitable or impossible. Rationed out of the short market, a trader might try to buy put options. But this strategy did not work either. The option market became delinked from the stock market; there were wide violations of put-call parity, precisely because arbitraging between stocks and options required shorting stocks.
The absence of an exploitable arbitrage is a little bit comforting, but it does not address the basic question: why were the prices so out of line in the first place? Lamont and Thaler's view is simply that there were a large number of "irrational" traders, who just did not see the chance to buy Palm embedded in 3Com, and for whom buying Palm rather than 3Com (and similar cases) was therefore "simply a mistake."
Intrigued by this paper, I investigated(3) the issue a bit further. 3Com and Palm remind me of money and bonds. Just as 3Com and Palm are both claims to Palm shares in six months, so money and a six-month Treasury bill are both claims to a dollar in six months. Yet the bill is cheaper and the dollar is "overpriced."
You might object that nobody holds money for six months. The whole point of money is that you hold it only for a short time, in order to make transactions. But few people held Palm for six months either. Lamont and Thaler document that 19 percent of available Palm shares changed hands every day in the first 20 days after the IPO, and several of their other cases have even larger volume. Furthermore, Palm had a 7 percent standard deviation of daily returns, or a 15 percent standard deviation of 5-day returns -- as much as the S&P500 moves in a year. If you can predict any of this movement, then the 2/10 percent per day expected loss due to "overpricing" is trivial; it's less than the commissions and bid-ask spread facing these active traders.
You might object that money is "special" because you need to hold it to make transactions. Palm stock was special too. To bet on information about Palm, you had to hold Palm stock. Even to
short Palm, you must first find a lender, borrow Palm shares, and then sell them. Options trading or trading in 3Com stock (3Com still held 95 percent of Palm shares) were poor substitutes, as both markets became delinked from high frequency movements in Palm stock market in this period.
Palm and money behave similarly in many other ways. Money is more overpriced -- the interest rate is higher -- when velocity is higher. The same is true for 3Com and Palm: the "overpricing" was highly correlated with Palm volume. The monetary overpricing (interest rate) is lower when the money supply is larger. The same is true for 3Com and Palm. Palm started with only 5 percent of total shares available, and less than that available for trading, because those receiving IPO allocations are strongly discouraged from flipping (selling) or lending their shares. Short selling provides an extra "supply" of shares, just as checking accounts provide extra money for transactions. Short selling in Palm built up quickly after the IPO. Palm peaked at 146 percent short interest -- the average share had been lent out to short more than once -- more than doubling the supply. As this supply increased, the overpricing fell. 3Com fell during the Palm IPO, even as the latter was exploding in value and even though 3Com still held 95 percent of Palm shares. With no horrible news about the rest of 3Com, this fall only makes sense if the Palm-information traders all coordinate on trading Palm shares, so that "convenience yield" for trading in Palm prospects suddenly moves to Palm and away from 3Com.
In sum, these observations suggest to me that trading generated a "convenience yield" for Palm shares, just as physical trading generates a convenience yield for money. People wanted to trade on information or opinions about the fortunes of Palm's invention, the PDA. To do this, they had to hold Palm shares, but Palm shares were in short supply. This "convenience yield" nicely links a large number of phenomena: 1) "overpricing" of seemingly identical securities; 2) "overpricing" is higher when volume is higher; 3) "overpricing" is higher when share supply is lower; 4) "overpricing" is higher when there are fewer substitutes for trading (options, correlated stocks) 5) "overpricing" is higher when there is more price volatility (a sign of more information flow); and 6) 3Com stock fell at the Palm IPO.
Most stories for 3Com-Palm are at best silent on points 2-6. In particular, "irrational investors" or "rational bubbles" do not link "overpricing" with volatility and volume, whereas all of the famous "bubbles" have featured tremendous turnover and volatility. If something about the psychology of evaluating risks makes traders irrationally attracted to Palm, why do 20 percent change their minds and resell their Palm shares on any given day?
You might object, "How could convenience yields or liquidity premia be that large?" First, recall that monetary "overpricing" can be quite large as well. In a 100 percent per year hyperinflation, currency trades at twice the value of six-month bills, and probably still with less than 20 percent daily turnover. Second, recall the Gordon growth formula: that the price-dividend ratio is the inverse of expected return less dividend growth, P/D = 1 (r-g). If a stock has a price-dividend ratio of 50, r-g = 0.02, so a single percentage point change in expected return can double the price if it's persistent. Liquidity premia of one percent or so are observed in the bond market, so one might not be surprised by substantial liquidity premia in stock prices.
Is this an isolated incident, or is a substantial "convenience yield" for trading an important part of stock valuation in general? Some simple facts in my paper suggest the latter possibility. In particular, "high price" stocks trade frequently, both in the cross section and in the time series. I run regressions across stocks of market value / book value on turnover (share volume / shares outstanding) and find large and significant coefficients; the correlation is between 0.25 and 0.35. The NYSE index and volume are correlated over time, dramatically so through the great crash of 1929. The correlation is impressive. With different labels, a monetary economist might happily point to a stable link between velocity (volume) and interest rates (price of money/price of bonds).
This well-known correlation usually is interpreted that price declines cause volume to dry up (for unknown reasons). For example, John M. Griffin, Federico Nardari, and Rene M. Stulz(4) show that volume is bigger after good returns, and markets "dry up" after bad returns. They interpret it this way. But perhaps some of the opposite is true as well: perhaps a decrease in the desire to trade (a decrease in information flow) or the ability to trade makes shares less valuable.
These patterns are not unique to Palm-3Com. Eli Ofek and Matthew Richardson(5) document that many of these features hold for the period of remarkably high price, volatility, and trading volume in the technology sector of the Nasdaq as a whole. One of their most interesting observations is that returns are negative around the expiration of many IPO's lockup period. (For some time after an IPO, insiders are typically forbidden to sell their shares. When the lockup expires, a large number of shares are released for trading or lending to shorts.) Furthermore, the price decline of the overall Nasdaq tech sector in March 2000 coincided with a large release of shares from lockup (see their Figure 2).
Short Sales Constraints
A central part of all "overpricing" stories is that there are limits to the ability of arbitrageurs to establish long-term short positions. If short sales are expensive, and the shorts are the "marginal investor" setting prices, we ought to see that stocks with higher short costs have lower subsequent returns.
Alas, good data on short costs are hard to come by. Owen Lamont and Charles Jones(6) use data from the 1920s, when rebate rates, one of the prime short costs, were published. They find lower returns for high-short-cost stocks, though not quite one-for-one. Lamont(7) shows that returns are lower among firms who engage in legal and technical battles that raise the cost of selling short. In both cases, the returns can be as much as 1-2 percent per month lower among firms with the highest short costs. Lamont and Jeremy C. Stein(8) use data on "short interest," the fraction of shares sold short. By itself, this is a poor (though often-used) measure of short costs, since it captures people who are able to short. Lamont and Stein use it indirectly to show that short interest declines as markets rise, suggesting that negative opinion is wiped out on the way up. In particular, they show that investors pull money out of open-ended (investors can add or withdraw at any time) short funds even though their string of losses only makes the short position more desirable. These three papers are summarized in more detail later in this issue.
One nagging question is, "If you can't short stocks, why not buy put options?" Lamont and Thaler document that Palm options and stocks became delinked -- there were massive violations of put-call parity. But is this an isolated, extreme case? Eli Ofek, Matthew Richardson, and Robert F. Whitelaw(9) claim otherwise. In fact, they find frequent violations in put-call parity that are strongly related to the cost of shorting. Their violations forecast subsequent low returns on stocks. (Battilio, Robert, and Paul Schultz(10) recently have questioned Ofek and Richardson's finding of put-call parity violations, claiming that the use of intraday options data, rather than closing quotes, resolves most of them. They do not address Ofek and Richardson's finding of negative expected returns however.)
Of course, documenting that short sales constraints prevent speculators from effectively lowering a price right away still leaves open the question, "Just why is the stock overpriced in the first place?" This is a job for theorists, and I describe some of their efforts below.
Liquidity Premia
Financial economists have long suspected that less liquid securities might have to offer an expected return higher than what is justified by the covariance of the security's return with the market or other factors. Thus the security might have a lower price level. (See Maureen O'Hara's Presidential Address(11) for a review.) The motivation traditionally has focused more on the price discount that an "illiquid" security might have relative to a frictionless market, rather than on "convenience yield," or a price premium that a security might enjoy for its special usefulness in allowing information trading. The issues are closely related, though.
Bonds
It's easier to see liquidity premia in bonds than in stocks, since the payoffs are known. Liquidity premia are clear in U.S. treasuries, for example, in the spread between on-the-run (just issued) and off-the-run issues. Seeing them in other, potentially much more illiquid bonds is harder, since a spread may be attributable to default as well as to liquidity.
Francis A. Longstaff(12) separates default from liquidity premia by comparing U.S. Treasury with Refcorp bonds. Most agency bonds (Fannie Mae, Freddie Mac) carry some small default risk, but Refcorp bonds do not: their principal is fully collateralized by Treasury bonds, and the Treasury guarantees full payment of coupons. Thus, they are identical to Treasury bonds in all aspects but liquidity (and, perhaps, obscurity). Longstaff finds that their average premia range from about 10 to 16 basis points of yield (0.10 to 0.16 percent). The premia vary significantly over time. The maximums range from 90 basis points for the three-month premium to about 35 basis points for the seven-year premium. These spreads may seem small, but small yield spreads can imply big price spreads for long-maturity bonds, up to 15 percent in Longstaff's data.
Longstaff, Sanjay Mithal, and Eric Neis(13) use the swap market to obtain market-price-based estimates of the default premium, and hence measure the residual liquidity premium. (One can now buy "default insurance" on particular bonds, and the premium for this insurance can be used to measure the default premium in a bond yield.) Most previous calculations suggested that corporate bond yields were much larger than default alone could account for, but Longstaff, Mithal, and Neis find otherwise: 51 percent of the yield spread of AAA/AA- bonds, 56 percent for A-, 71 percent for BBB, and 83 percent for BB- are explained by default premia measured in the credit-default swap market. However, a substantial residual remains, between 20 to 100 basis points. This component is strongly related to measures of liquidity, such as the size of the bid/ask spread and the principal amount outstanding.
Stocks
Lubos Pastor and Robert F. Stambaugh(14) find that stocks whose prices decline when the market gets more illiquid receive compensation in expected returns. Dividing stocks into ten portfolios based on liquidity betas (regression coefficients of stock returns on market liquidity, with other factors as controls), the portfolio of high-beta stocks earned 9 percent more than the portfolio of low beta stocks, after accounting for market, size, and value-growth effects with the Fama-French 3 factor model. Almost all of this premium is accounted for(15) by the spread in liquidity betas and a factor-risk premium estimated across ten portfolios.
Viral V. Acharya and Lasse H. Pedersen(16) perform a similar but more general investigation. They examine all four potential channels for a liquidity premium. First, a security might have to pay a premium simply to compensate for its particular illiquidity or transactions cost, but this is the least interesting (and, as we will see in the theory discussion, least likely) effect. Second, a security might have to pay a premium because it becomes more illiquid in bad times, such as when the market goes down. If you have to sell the security, (and if sellers are the marginal investors) this tendency amounts to a larger beta than would be measured by the midpoint of a bid-asked spread. Third, the security's price (the midpoint) might decline when markets as a whole become less liquid. If "market liquidity" is a state variable, an event that drives up the marginal utility of a marginal investor, then this tendency also will result in a return premium. This is the mechanism that Pastor and Stambaugh investigated. Fourth, the security could become more illiquid when the market becomes more illiquid. Of course these characteristics are correlated in the data, which makes sorting out their relative importance more difficult.
Acharya and Pedersen form 25 portfolios sorted on the basis of previous year's liquidity (the liquidity of the individual stocks, this time, not Pastor and Stambaugh's regression coefficient of return on market liquidity). They find that average returns range from 0.48 percent to 1.10 percent per month as the illiquidity of the portfolios rises. However, their measure of illiquidity is (intentionally) highly correlated with size, and the size ranges from 12.5 to 0.02 billion dollars in the 25 portfolios. Then, they examine whether the four sources of covariation described above explain the variation in average returns. The illiquidity covariances are significant in some specifications. Interestingly, their most important effect (the largest and most significant premium in a cross-sectional regression of average returns on betas) is the covariance of liquidity with market return -- the chance that the stock may get more illiquid if the market goes down.
While both papers find that liquidity betas do correlate with average returns, and both have some success in explaining the expected returns of portfolios sorted on liquidity measures, neither paper claims that "liquidity betas" are a complete description of stock returns. Neither model explains the average returns of portfolios sorted on book-to-market, size, or past-returns-by-liquidity betas alone. This is not a failing; in fact, it is predicted by Acharya and Petersen's model, in which liquidity premia operate above and beyond the usual CAPM. It just means that we will have to understand liquidity as an additional feature, above and beyond the usual picture of returns driven by the macroeconomic state variables familiar from the frictionless view.
Looking a little more deeply into the making of this sausage will show some of the achievement of these papers, and some of the challenges that remain. The biggest challenge is how to measure liquidity (and to some extent, how to define liquidity) both at the individual-stock level and at the market level. Larger bid-ask spreads and transactions costs are indicative of course, but a larger sense of liquidity really matters: how much is for sale at the bid-ask points ("depth"), and most of all how large will the "price impact" of a trade be.
Pastor and Stambaugh's basic idea is that stocks are "illiquid" if there is a large price-impact of orders. A big "buy order" in an illiquid stock should result in large volume and negative return, but this event should forecast a positive return the next day as the price "bounces back." To measure this tendency they run a regression(17) over days in each month of the return at day d+1 on a constant, the return at day d to allow for a "normal" serial correlation of returns (though I'm not sure where that comes from) and the product of volume on day d times the sign of the return on day d. The size of the (negative) coefficient on the last variable measures the stock's "liquidity" for the month. Pastor and Stambaugh want innovations in market liquidity. (The paper is about risk as measured by regressions of individual returns on market liquidity, not about individual-stock liquidity.) They measure this quantity by calculating innovations to the changes in the average liquidity of individual stocks, scaled by the growing size of the market.(18)
Acharya and Pedersen define the liquidity of a stock in each month as the average absolute return divided by dollar volume in that month(19). This measure looks only for price changes at date d, whereas Pastor and Stambaugh look for a bounce-back, predictable price changes in the return from d to d+1. Acharya and Pedersen thus measure "price discovery," people buying today on the knowledge that the price will rise tomorrow, rather than just "price impact." This raw measure leaves a size effect - as inflation increases dollar volumes, illiquidity defined from returns divided by dollar volume apparently decreases. To remove the size effect over time, they scale the raw illiquidity measure by the market capitalization in each month, and they trim outliers.(20) This measure leaves intact the cross-sectional scaling of "illiquidity" with size: smaller stocks which have smaller dollar volume for the same turnover (fraction of outstanding shares that trade) are automatically more illiquid. While one might argue that small stocks are more illiquid, it does mean the results flow from the well-known (and possibly liquidity-driven) size effect in returns.
Having seen the details, it's clear that these authors are grappling with deep conceptual problems in very sophisticated ways - but that a cleaner definition and measurement of "liquidity," though obviously a difficult objective, will be a valuable one.
Order Flow, Price Impact, and Downward Sloping Demand Curves
One indication of "illiquidity" or "convenience yield" is "price impact" or a "downward sloping demand curve" for stocks. A non-financial economist, quite used to downward-sloping demand curves, might be puzzled why we even worry about this question. After all, if you show up with a truckful of tomatoes in Harvard Square at 2:00 AM determined to sell them in the next half hour, you're not going to get a very good price. There are arbitrageurs hanging around financial markets, of course, but even they have limited capacity to bear risk.
However, if the sale is announced, or so regular that it becomes expected, then arbitrageurs should know to show up, so the presumption leans much more to a flat "demand" (in quotes because half the time it's "supply") curve. For this reason, we should be more surprised to see "price impact" of regular or expected sales or purchases in a frictionless market.
Market microstructure models have an additional story for price-impact: asymmetric information. If you offer to sell a lot of stock unexpectedly, this might mean you know something that the traders don't, and they will therefore only offer a lower price. Thus, we are more surprised to see price-impact of regular, expected, or otherwise information-free trading.
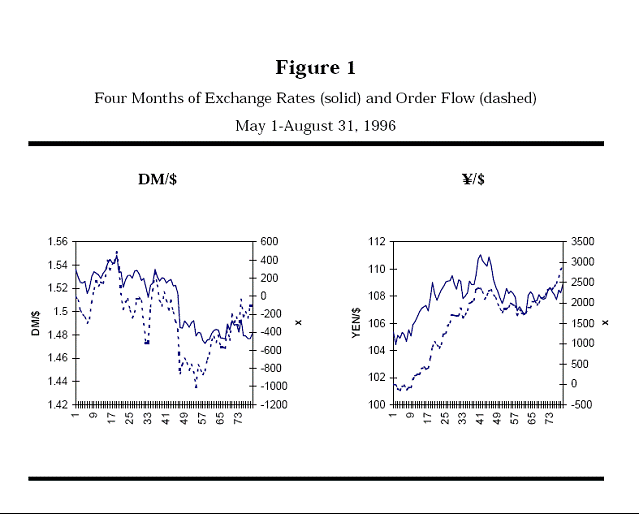
Martin D.D. Evans and Richard K. Lyons(21) show that exchange rate movements are highly correlated with order flow. I reproduce Figure 1 from their paper here. The solid lines are the spot rates of the DM and Yen against the Dollar. The dashed lines are order flow. The correlation is impressive.
A difficulty in most studies of this sort is that you typically do not know if a trade is a "buy" or a "sell," and in fact we routinely make fun of journalists who report a wave of "buying" since every "buy" must correspond to a "sell." Evans and Lyons's dataset does record which side initiated the transaction, so "order flow" can be measured and does make some sense. (Many studies rely on whether the trade takes place above or below the midpoint of the bid-ask spread to identify the sign of the trade, but direct measurement is obviously much cleaner.)
Evans and Lyons interpret the correlation as causal, in other words that order flow causes the exchange rate to move. In this paper and "A New Micro Model of Exchange Rate Dynamics"(22) they provide rich theoretical models that produce this sort of effect. The latter model combines standard general equilibrium models (productivity shocks, consumption, investment, capital formation) with microstructure in the exchange market, in particular that agents know more about their home shocks than foreigners.
Michael W. Brandt and Kenneth A. Kavajecz(23) perform a similar and much more detailed analysis in the market for U.S. Treasury bonds. Brandt and Kavajecz have trade-by-trade data in government bonds from the GovPX system on which the bonds are traded. They also know who initiated the trade -- whether is it a "buy" or a "sell." With all quotes at a given time, they can measure bid-ask spread and depth; how much is for sale at what price.
Brandt and Kavajecz aggregate bonds into maturity bins and on-the-run, just off-the-run and off-the-run status. (Newly issued bonds are said to be "on the run." They are most actively traded, since they make their way from the government to long-term holders such as pension funds. Trading in off-the-run bonds can be quite thin as many U.S. treasury investors are passive.) Brandt and Kavajecz run regressions in daily data of yields in these classes on lagged yield curve factors (level, slope and curvature, linear combinations of lagged yields) and order flows. In each case, yields on day d+1 are significantly related to order flow between day d and day d+1, with R2 nearing 30 percent. For yields of class i, orderflow of that class is the most important forecaster. Interestingly, other orderflows enter as well. Order flow in the 2-5 year maturity is the most important other class in each case. A single common factor (essentially the average of order flows across all maturities) in order flows across all yields also compactly captures the cross-effects.
To examine how orderflow affects the overall shape of the yield curve rather than individual bond yields, they regress factor portfolios (the average of all yields = level, and other linear combinations for slope and curvature) on order flows of different classes of bonds. They find that the "level" factor, the average of all yields, is most influenced by order flow. Order flows across all maturities forecast changes in the level of interest rates, and a common "level" factor in order flow moves the common "level" factor in yields with nearly the same R2 as the multiple regression using order flows on all maturities. Other factors are much less related to order flow, let alone factors in order flow. For example, there does not seem to be a "slope" factor in order flow (buy short, sell long) that induces changes in the slope of the yield curve. Interestingly, the effects are stronger for liquid on-the-run bonds rather than less liquid off-the-run bonds.
Brandt and Kavajecz interpret their findings as evidence for "price discovery" rather than for "illiquidity" or "price impact." In a market of symmetric information, that information raises prices without any trading. In a market with asymmetrically informed agents, those with the information will trade on that information as prices rise, so that price rises and buy orders will be correlated as we see. "Price discovery" makes sense of the fact that orderflow of other classes helps to forecast yield changes in class i. This would not happen if traders were simply pushing on class-specific demand and supply curves. In addition, "price discovery" makes sense of the fact that order flow in the liquid on-the-run bonds is the important one for forecasting returns.
Kenneth A. Froot and Tarun Ramadorai(24) correlate exchange rates with flows between institutional investors. Again, they exploit a dataset that shows all purchases and sales, so they know the direction of the "flow." They find that daily flows exhibit a correlation with daily excess returns of about 30 percent.
Froot and Ramadorai undertake a dynamic analysis and uncover "trend-following" by managers: a 1 percent surprise appreciation results in a 0.37 standard deviation inflow over 30 trading days, for the major currencies in the sample. Consistent with this finding, the flow/return correlation rises strongly with horizon, peaking at about 45 percent at horizons of about a month. The flow/return correlation then declines rapidly with horizon. In long horizons, the authors find that fundamentals, not flows, drive exchange rates.
In sum, we have a striking fact: order flow is highly correlated with price changes. We also have three interpretations of this correlation. 1) Perhaps order flow causes the price change, simply running into the illiquidity, "downward sloping demand," or "limited ability to bear risk" of
marketmakers. 2) Perhaps "price discovery" causes the correlation; informed investors come in and bid up prices to where they will go once the information becomes public, and do a bit of trading on the way. 3) Perhaps causality runs backwards: perhaps prices change, and then "trend-following" and "momentum" traders pile volume in that direction. The cross-asset correlations and dynamics suggest the second and third interpretations, though it is possible that a big order into one class causes disruptions in another. I look forward to a detailed cross-sectional and time-series analysis to add evidence that will sort these hypotheses out. At a minimum, the second and third interpretations argue that we need to understand where order flow comes from before concluding that it causes price changes.
Nicholas Barberis, Andrei Shleifer, and Jeffrey Wurgler(25) extend a long line of research on S&P500 inclusion effects suggesting "downward sloping demand curves." They find that stocks start to comove more with the S&P500 index as soon as they are included in that index. In single regressions, daily betas (regression coefficients of stock return on S&P500 index return) increase by 0.15 and weekly betas increase by 0.11 upon inclusion (that is, a typical regression coefficient increases from 1.0 to 1.15). Considerations such as non-trading and lagged betas weaken the magnitudes and statistics a bit, but do not eliminate the effect. In a nice refinement, these authors run regressions of individual stocks on both S&P500 and non-S&P500 stocks. The coefficients on S&P500 rise more, up to 0.3, and those on non-S&P500 decline on inclusion, although the standard errors are somewhat wider because the right-hand variables are highly correlated. Monthly betas do not increase, with the interpretation that short-run demand curves slope down but long-run curves do not. There is a natural source of volume that occurs upon S&P500 inclusion: index arbitrage of individual stocks versus the index and S&P500 options, and demand from S&P500 index funds. But since these are a predictable source of trading, it is surprising that they run into any illiquidity.
Economic Models
So far I have written as if we had good economic models of trading, liquidity, convenience yield, and so on. Of course nothing of the sort is true. Solid economic understanding of all of these issues, and even clear definitions or verbal stories, remain a challenge.
Two fundamental stumbling blocks stand in the way. First, why is there so much trading? It's no mystery to the layman; people are trading on information and opinion. But economic models of information-based trading quickly stumble on the "no-trade theorem." Paul Milgrom and Nancy Stokey(26) show that rational traders should act like Groucho Marx, who famously didn't want to belong to any club who would have him. Anyone who wants to sell to you knows something you don't know. Not everyone can be smarter or better informed than the average.
Second, models of illiquidity premia fundamentally stem from transactions costs. But agents solving typical portfolio problems can avoid transactions costs easily by refusing to trade very often, a point made most famously by George M. Constantinides(27). As a result, large transactions costs typically have small price effects. The two points are related. The classic theory of finance doesn't give much of a reason to trade, so it naturally does not assign much of a penalty for assets that are hard to trade.
As I review theory papers designed to understand volume and liquidity premia, you will see a variety of unpalatable devices used to avoid these two fundamental barriers. For example, no-trade theorems are often broken by sprinkling in some "noise traders" who buy or sell for unspecified reasons unrelated to information. You will see models with "optimists" and "pessimists" who have different prior beliefs unrelated to any information, or who irrationally overweight their own information. You will see models that crank up lifecycle or hedging motives for trade to unreasonable levels in order to generate some volume. For example, one writes a model with agents that last two months, so each must buy and sell his entire portfolio in two months. Another posits that investors exogenously withdraw funds from managers after poor returns. Another introduces random preference shifts.
How one interprets these ingredients is a matter of philosophy. Some people see them as proof that finance needs to abandon economics for its behavioral foundations, and thus the assumptions are worth advertising or fussing about, depending on one's views on that question. I tend to see them as sensible shortcuts, quick modeling tricks where starting from "deep microfoundations" would waste too much time and space on the way to the phenomenon we want to capture, and thus they are not worth making much of a fuss about either way. I find it hard to swallow the proposition that there can never be any model built on economics in which the NYSE and NASDAQ exist, but I don't want to wait for its construction to start thinking about the economics of liquidity. In a similar way, macroeconomists write models with cash-in-advance constraints, money in the utility function, sticky prices and so on, not because they believe literally in these specifications but as a convenient shortcut to a money demand curve on the way to studying something else, without waiting for the "microfoundations of money" project to be finished. Buttressing this view that not much essential is at stake, it seems pretty clear in most cases that assumptions could easily be substituted with no effect on the basic results. Most models just need some, any reason for trade. Similarly, the liquidity models just postulate transactions costs rather than derive a bid-ask spread from asymmetric information, and happily go on.
Of course, this state of affairs means that the answers are not fully satisfactory until the microfoundations of trade really are understood. You never know for sure that a shortcut leads to the right road unless you have a full map, and deeper models will be an ongoing project. At any rate, a look at the current crop of models will give the reader a better sense of where these devices fit in, how to interpret them, and what a really satisfactory model of volume, information trading, and liquidity might look like.
Convenience Yield, Short Sales, and Search
Darrell Duffie, Nicolae Garleanu, and Lasse Pedersen(28) describe a model that captures many of the 3Com - Palm and short-sales constraint phenomena. This model is of pure shorting. Relatively optimistic agents hold the security only to search for a relatively pessimistic agent who will borrow it, and then sell it to a relatively optimistic agent again.
A security has an unknown value at some random date in the future. Some agents are "optimists" and some are "pessimists." They have different prior views on this value, rather than different information, sidestepping the no-trade theorem. Shares are traded by a Walrasian auctioneer in a centralized market at each moment. To sell short, however, a pessimist must first locate another agent from whom to borrow the shares. The search proceeds by random matching. When a pessimist meets an optimist, they engage in Nash bargaining over the borrowing fee or rebate rate. The model starts, as after an IPO, with no short interest.
At any time, optimists are willing to pay more than even they think the stock is worth, because they can earn fees from lending shares out to shorts. (This is the heart of Jones and Lamont's findings described earlier.) In fact, it is rational for them to buy shares at "too high prices" and then hold them for some time as they search for a short to whom to lend the shares. Thus, in this market everyone thinks shares are overvalued at current prices, but they hold them nonetheless, waiting to find someone to lend them to for short sales. As one might expect, price and volume decrease over time, and short interest increases, exactly the pattern we see in 3Com-Palm.
Lending fees are larger if the difference of opinions is larger, and the price and lending fee are higher if the float is smaller. The overpricing is more drawn out if one has to wait 3 days for settlement before lending out a share again, as well as search for new borrowers. The model does not generate volatility and much volume however; the only volume is the expanding lending, selling short, and lending again.
In "Over-the-Counter Markets," (29) these same authors present a related matching and search model. The focus of this paper is on bid-ask spreads, and the point is to develop a theory of these spreads completely different from the standard one. In the standard theory, dealers hold an inventory of the asset, and manage the bid-ask spread to control this inventory and to control asymmetric information, that is, the chance that an "informed" trader will take advantage of the dealer. This model has no inventory and no asymmetric information.
The setup corresponds to the many assets that are at least partially traded over the counter. Agents randomly switch between low and high discount rates, motivating trade of a single claim to future consumption. (When you get more impatient, you sell to consume now). In addition, there are marketmakers who can instantly unload their positions on the inter-dealer market. Agents meet randomly. The bid-ask spread reflects the dealer's bargaining power versus the investors' other options -- how easily he can find another investor to trade with, or another dealer. For example, spreads charged by dealers will be lower the easier it is for investors to find other investors in the over-the-counter market.
Wei Xiong, Harrison Hong, and José Scheinkman(30) present another model aimed at the curious features of the late 1990s Nasdaq, and Ofek and Richardson's finding that prices decline at the end of lockup periods in particular. They study a mechanism by which small float and short sales constraints lead to "overpriced" securities, a "bubble" in prices, defined for them as a situation in which agents rationally buying stocks they know to be overpriced on the expectation of further price rises, high turnover, and high volatility. All of these features decline when float increases, even when it is known in advance that float will increase.
There are three periods: 0, 1, and 2. An asset has a random payoff in period 2. Two investors are each endowed with half of the shares and they have identical mean-variance utility functions over terminal wealth. They may trade at period 0 or 1, but are subject to short sales constraints. At period 1 they each receive a signal about the asset payoff. The signals are public, but each investor is "overconfident" about "his" signal, thinking it more correlated with the true payoff than it really is. As a result, the (ex-post) "optimist" will buy from the "pessimist" in period 1. Since they face short-sales constraints, there will be values of the signals for which one agent holds everything, and the period 1 valuation depends entirely on his signal. Working back, Xiong, Hong, and Scheinkman show that the price at time 0 will be larger than both agents' expectations of fundamental value at time 0. They are both willing to pay for the "resale option" that an "overconfident" agent comes along and bids the price up even further. To the authors, this captures the essence of a "bubble".
As the share size increases, the overall price in periods 0 and 1 decreases. This is the only asset, so each agent has to bear more risk. It also then becomes less likely that in period 1, after information is revealed, one or the other agent hits his short-sale constraint. If nobody hits the short-sale constraint, the "resale option" disappears. Conversely, with a very small share size, it becomes almost certain that one or the other agent will hit his short-sale constraint and therefore the asset will be "overpriced" in period 1. (Here quadratic utility is important. Were it log utility, nobody would ever want to be short.) Thus, "overpricing" is greater when share supply is lower, as Lamont and Thaler find for 3Com-Palm and as Ofek and Richardson find around lockup expiration in the Nasdaq.
Furthermore, as the share supply gets smaller, it becomes more and more certain that one agent will sell all of his shares to the other. Thus proportional turnover (not dollar turnover) is larger when share supplies are smaller. Similarly, price volatility is higher.
Xiong, Hong, and Scheinkman go on to show that the model continues to work in a multiperiod setting in which the agents know that a lockup expiration will add shares to the market. Thus, a predictable fall in price when shares predictably increase, a "downward sloping demand" of the puzzling sort, emerges.
Liquidity and Quality Premia
Acharya and Pedersen(31) present a model along with the empirical work I described earlier, and the model captures the four variants of a liquidity premium: in addition to the standard market beta, expected returns are higher for stocks that are illiquid on average, for stocks whose illiquidity gets worse when the market goes down, for stocks whose price goes down when the market gets more illiquid, and for stocks which become more illiquid when the market gets more illiquid.
The model consists of overlapping generations. Agents live two periods, earn income in the first period, and consume in both periods. Thus they buy securities when young and sell them when old. Agents in a generation also have different risk aversion. "Illiquidity" is simply a random security-specific per-share cost of selling each security -- sellers receive the price less the cost per share. "Market illiquidity" is then just the value-weighted average of these costs. Securities are claims to dividend streams, and both dividends and the costs follow AR(1) processes.
The theory then is quite simple: since every agent liquidates his portfolio in the second period of his life, the CAPM holds exactly using returns after transactions costs. Simply expanding the standard expression of the CAPM that expected (return - cost) is proportional to the regression beta of (return - cost) on the (market return - cost), we obtain that expected returns rise with the expected cost of the individual security and the four "betas" listed above. Furthermore, since liquidity (transactions cost) is persistent, the model generates time-varying expected returns predictable on the basis of liquidity variables. (This is an important point. Many of the most popular trading strategies used by hedge funds and similar traders exploit return predictions based on the intersection of past returns and volume data.)
Dimitri Vayanos(32) is motivated by another striking recent event, the "flight to quality" or "flight to liquidity" following the Russian bond default in 1998. This event seems to provide a paradigm of liquidity issues. For example, the on-the-run versus off-the-run 30-year U.S. Treasury spread widened from 4 basis points (0.04 percent) to 28 bp. The spread between AA-rated corporate bonds and government bonds increased from 80bp to 150bp. At the same time, prices became much more volatile. For example, the implied volatility of the S&P500 index increased from 23 percent to 43 percent.
Naturally, "spread traders" who were typically short liquid securities (for example, on-the-run 30 year bonds) and long the illiquid ones (for example, off-the-run 29-year bonds) suffered huge losses. Withdrawals by investors as well as margin calls forced liquidations at unfavorable prices. The losses were made worse by seemingly uncorrelated assets becoming more correlated, revealing a common "liquidity factor" in returns. LTCM was the most famous casualty. Certainly these traders would have given up a lot of utility for a dollar delivered in that date and state, motivating a "risk premium" for assets that do not do so.
Vayanos presents a very sophisticated (in the sense that lots of things are endogenous) model that shows how illiquidity is linked to volatility, and that captures the larger betas and correlations of assets in times of high volatility and illiquidity. Investors in this model are all fund managers, and they earn a fixed fraction of assets under management. They face fixed asset-specific transactions costs. They also face the danger of a total withdrawal of funds. The chance of such a withdrawal is a linear function of the probability of achieving a return below a certain threshold, and is thus an increasing function of the fund's volatility. After withdrawal, the manager gets to start a new fund of the same size as the old one right away. Thus the "withdrawal" simply means that the manager may have to pay the transactions costs (liquidation value - net asset value) and the model is formally equivalent to one with representative consumer-investors who face random liquidation events (more likely with higher volatility) in which they have to pay the transactions costs and then reinvest. The model is completed with the dividend processes of n risky assets that mean-revert, and have stochastic volatility (square root processes). The dividends are driven by a common shock, a volatility shock and an idiosyncratic shock.
One result is an expected return model with liquidity and volatility effects. The expected return of each asset depends, first, on covariances with the market return (CAPM), but with a time-varying risk premium that is higher in times of volatility. Second, expected returns depend on the covariance of the asset with the volatility of dividend growth, again with a time-varying risk premium. Finally, the expected return of each asset rises if the transactions cost of that asset are higher, but again with a coefficient that is larger when volatility is larger. In each case, higher (exogenous) volatility of dividends, and hence of returns, increases the chance of withdrawals; the fund managers then require higher returns.
The model also predicts that conditional market betas vary through time, and their spread across assets is larger when volatility is higher. It also predicts that the correlation between assets typically increases in times of higher volatility. These properties flow from the assumption that the probability of withdrawals depends linearly on poor performance - the left tail of the return distribution. The chance of a left-tail event is a nonlinear function of volatility. When volatility is low, the chance is low and slowly increasing in volatility. When volatility is high, the chance of poor performance runs into the steeply sloping part of the conditional density, and so has a large effect.
The model suggests a theory for a "liquidity pricing factor" such as found by Pastor and Stambaugh. While the transactions costs (bid-ask spread) in the model are constant for each asset, in a time of higher volatility small generalizations of the model suggest higher "price impact," which forms the basis of Pastor and Stambaugh's aggregate liquidity factor.
Bryan R. Routledge and Stanley E. Zin(33) offer a different and frictionless interpretation. Many "flights to quality" have come after extreme market movements, movements that put to the test sophisticated traders' hedging models, and found them failing. In their frictionless view, bid-ask spreads widen when agents become more uncertain about the validity of their models.
Francis Longstaff(34) presents another model of liquidity and flight to quality. The model has two "Lucas Trees." There also are two agents, one more impatient than the other. They can trade at time zero, but then they cannot trade for T periods. The length of this "blackout" period is the concept of illiquidity in the model. Longstaff solves for the resulting prices of the two trees.
In this model, the portfolio allocations can be quite different under illiquidity, even if that illiquidity is arbitrarily short-lived. The reason is that a log-utility investor can never have a short position in an asset for a finite time interval, as he then faces a probability of negative wealth. The impatient consumer therefore cannot borrow. Rather than hold the market portfolio of the two trees, agents now hold very polarized portfolios. The change in demand also has large effects on the prices of the two assets.
Anthony Lynch and Sinan Tan(35) tackle the low-volume problem and the Constantinides puzzle head-on. They consider a standard portfolio problem. They add predictable returns, another reason for individual or heterogenous investors to trade. They add a stochastic labor income process, calibrated to PSID data, and wealth shocks to give a dynamic hedging motive. Finally, they introduce transactions costs to distinguish liquid and illiquid assets. Some calibrations of the model give liquidity premia in the ballpark found by Pastor and Stambaugh and Acharya and Pedersen. Of course, being partial equilibrium, we're not sure who is on the other side of all this trading, or why things like predictable returns persist.
Volume and Liquidity
Andrew W. Lo, Harry Mamaysky, and Jiang Wang(36) construct a model of volume and liquidity. At heart they study how transactions costs reduce volume and induce a price discount.
As always, we first need some reason for agents to trade in the first place. (The puzzle is that there is too much volume, not too little.) Lo, Mamaysky, and Wang achieve this by giving agents a nontradeable risky asset -- a business, a job, et cetera. The outside income is correlated with the stock market, so the agents want to hedge it. As the outside income increases or declines in value, the optimal hedge changes, giving the agents a reason to trade continuously. Adding transactions costs, the agents trade less frequently, in discontinuous lumps. As a result, the agents bear more risk, and so demand less of the risky asset. Then, the risky asset has a price ("illiquidity") discount. This discount is approximately proportional to the square root of the transactions cost, so it is large for small costs.
Specifically, Lo, Mamaysky, and Wang model two agents in continuous time. The only assets are a stock -- a claim to a random walk dividend -- and a riskless bond. The "outside income" is a claim to the same dividend process, but the size of this claim also varies as a random walk. There is one kind of tree in the valley, so all trees bear the same amount of fruit. Some trees live in the orchard, and agents trade claims to those trees. Some trees are constantly uprooted from one agent's yard and planted in the other's yard. The lucky guy who got the tree will then want to sell some stock (claims to the orchard) to the unlucky guy who lost the tree. He keeps his increased wealth, but the right risk exposure gets reestablished in this way. The (substantial) technical achievement of the model is to solve for the agents' trading policies (a band of inaction) and the equilibrium asset price when there is in a addition a fixed (per trade, not per share) transactions cost.
The perfect correlation of "outside income" with the stock seems artificial, but components of outside income uncorrelated with stocks generate no hedging demand. Therefore, this is a useful simplification so long as one's quantitative evaluation of the model recognizes that this is the component of income correlated with stocks and not the whole thing.
Andrew W. Lo and Jiang Wang(37) continue an exploration of volume motivated by dynamic hedging. They write a model with investors who vary in risk aversion, and in sensitivity to a second, non-market state variable. (For example, older investors may care less than younger investors about a decline in short term interest rates, which lowers prospective returns to investment.) As a result, investors continuously trade both the market portfolio and a hedge portfolio for this state variable. Then Lo and Wang identify the composition of the hedge portfolio by looking for factor structure in volume.
I think the best way to think of these papers is to regard outside income and hedging as useful shortcuts to generate some trading. Then, the point of the paper is how transactions costs reduce trading and induce price discounts. I do not think they are useful models of why there is so much trading in the first place. Each share on the NYSE turns over on average about once per year. Twenty percent of Palm shares changed hands every day. Hedging non-marketed income or hedging state variables seems to me a hopeless starting point for a realistic and quantitatively compelling understanding of such massive turnover.
Perhaps in response to this sort of doubt, Guillermo Llorente, Roni Michaely, Gideon Saar, and Jiang Wang(38) examine the dynamic relation between volume and returns to try to separate volume into "hedging" and "speculative" components. They run regressions of daily individual-stock returns on the previous day's return and on the previous day's return multiplied by volume. They argue that a positive coefficient on lagged return times volume indicates "speculative trade": informed investors know that tomorrow's return (on the left hand side) will be large; they buy on that knowledge sending today's return up a bit and creating some volume in the process. By contrast, a negative coefficient on return times volume represents "hedging trade." Agents selling in to a market without information will push the price down temporarily, so a low return today times volume will presage larger returns tomorrow as the price bounces back. This is the same idea as in Pastor and Stambaugh's liquidity measure. (And as in that case, lagged returns on the right hand side means we are controlling for "regular" serial correlation in returns, which gives me pause.) The main finding is straightforward. Stocks with higher bid/ask spreads and smaller size -- proxies for larger "information asymmetry" -- have large positive coefficients on return times volume, suggesting "speculative" trade. Large stocks with small bid/ask spreads have negative coefficients suggesting more "hedging" motives.
Concluding Comments
Exchanges exist to trade stocks and bonds, and most of that trade occurs on information. For a long time, we have presumed that this trading activity has at best a second-order effect on the level of asset prices. Now both empirical work and theory are pointing to the exiting possibility that it is not; that a substantial portion of level and variation of asset prices, both over time and across assets, may reflect how those assets are used in trading.
This study is in its infancy. You can see empiricists struggling with definitions of liquidity and how to see its effects. You can see theorists struggling to formalize the intuition that liquidity and trading should matter, and to overcome the classic theorems that rule out information trading and give small effects of trading costs. But infants grow quickly, and it is a time of great progress on both fronts.
2. O. A. Lamont and R. H. Thaler, "Can the Market Add and Subtract? Mispricing in Tech Stock Carve-Outs," NBER Working Paper No. 8302, May 2001, and Journal of Political Economy, 111: pp. 227-68.
3. J. H. Cochrane, "Stocks as Money: Convenience Yield and the Tech-Stock Bubble," NBER Working Paper No. 8987, June 2002, and in W. C. Hunter, G. G. Kaufman, and M. Pomerleano, eds., Asset Price Bubbles, Cambridge: MIT Press, 2003.
4. J. M. Griffin, F. Nardari, and R. M. Stulz, "Stock Market Trading and Market Conditions" NBER Working Paper No. 10719, September 2004.
5. E. Ofek and M. Richardson, "DotCom Mania: The Rise and Fall of Internet Stock Prices" NBER Working Paper No. 8630, December 2001, and in Journal of Finance, 58 (2003), pp. 1113-37.
6. C. Jones and O. A. Lamont, "Short Sale Constraints and Stock Returns," NBER Working Paper No. 8494, October 2001, and in Journal of Financial Economics, 66 (3-3) (2002), pp. 207-39.
7. O. A. Lamont, "Go Down Fighting: Short Sellers vs. Firms," NBER Working Paper No. 10659, July 2004.
8. O. A. Lamont and J. C. Stein, "Aggregate Short Interest and Market Valuations," NBER Working Paper No. 10218, January 2004, and in American Economic Review, 94 (2) (May 2004), pp. 29-32.
9. E. Ofek, M. Richardson, and R. F. Whitelaw, "Limited Arbitrage and Short Sales Restrictions: Evidence from the Options Markets," NBER Working Paper No. 9423, January 2003, forthcoming in Journal of Financial Economics.
10. R. Battilio and P. Schultz, "Options and the Bubble," manuscript, University of Notre Dame, 2004.
11. M. O'Hara, "Presidential Address: Liquidity and Price Discovery," in Journal of Finance, 58 (2003), pp. 1335-54.
12. F. A. Longstaff, "The Flight-to-Liquidity Premium in U.S. Treasury Bond Prices," NBER Working Paper No. 9312, November 2002.
13. F. A. Longstaff, S. Mithal, and E. Neis, "Corporate Yield Spreads: Default Risk or Liquidity? New Evidence From the Credit-Default Swap Market," NBER Working Paper No. 10418, April 2004.
14. L. Pastor and R. F. Stambaugh, "Liquidity Risk and Epected Stock Returns," NBER Working Paper No. 8462, September 2001, and Journal of Political Economy, 111, pp. 642-85.
15. The canonical asset pricing model states that expected returns should be proportional to the regression coefficients of returns on pricing factors,
. Thus, a spread in average returns
across portfolios i is explained if they are linearly related to the betas
. For example, researchers often run a regression across assets of
on
and test whether the slope coefficient
is significant.
16. V.V. Acharya and L. H. Pedersen, "Asset Pricing with Liquidity Risk," NBER Working Paper No. 10814, October 2004.
17. The regression is
where r = return,
= return in excess of market return, and v = dollar volume.
18. To be specific, they calculate
where m denotes total market value. Their measure of "market liquidity" is
.
19. Their raw measure of the illiquidity of stock i for month t is
=
where R denotes return and V denotes dollar volume.
20. Their final measure of liquidity of stock i for month t is
where
is an index of the capitalization of the total market portfolio.
21. M. D. D. Evans and R. K. Lyons, "Order Flow and Exchange Rate Dynamics," NBER Working Paper No. 7317, August 1999, and Journal of Political Economy, 110, pp. 170-80.
22. M. D.D. Evans and R. K. Lyons, "A New Micro Model of Exchange Rate Dynamics," NBER Working Paper No. 10379, March 2004.
23. M. W. Brandt and K. A. Kavajecz, "Price Discovery in the U.S. Treasury Market: The Impact of Orderflow and Liquidity on the Yield Curve," NBER Working Paper No. 9529, March 2003, and forthcoming, Journal of Finance, December 2004.
24. K. A. Froot and T. Ramadorai, "Currency Returns, Institutional Investor Flows, and Exchange Rate Fundamentals," NBER Working Paper No. 9101, August 2002.
25. N. Barberis, A. Shleifer, and J. Wurgler, "Comovement," NBER Working Paper No. 8895, April 2002, forthcoming in the Journal of Financial Economics.
26. P. Milgrom and N. Stokey, "Information, Trade and Common Knowledge," Journal of Economic Theory, 26 (1982), pp. 17-27.
27. G. M. Constantinides, "Capital Market Equilibrium with Transaction Costs," Journal of Political Economy, 94 (1986), pp. 842-62.
28. D. Duffie, N. Garleanu, and L. H.Pedersen "Securities Lending, Shorting, and Pricing," Journal of Financial Economics, 66 (2002), pp. 307-39, presented at Spring 2001 Asset Pricing Program Meeting.
29. D. Duffie, N. Garleanu, and L. Heje Pedersen, "Over-the-Counter Markets," NBER Working Paper No. 10816, October 2004, previously "Valuation in Dynamic Bargaining Markets."
30. W. Xiong, H. Hong, and J. Scheinkman, "Asset Float and Speculative Bubbles," presented at the Fall 2003 AP Program Meeting.
31. V. V. Acharya and L. H. Pedersen, "Asset Pricing with Liquidity Risk."
32. D. Vayanos, "Flight to Quality, Flight to Liquidity, and the Pricing of Risk" NBER Working Paper No. 10327, February 2004.
33. B. R. Routledge and S. E. Zin, "Model Uncertainty and Liquidity," NBER Working Paper No. 8683, December 2001.
34. F. A. Longstaff, "Financial Claustrophobia: Asset Pricing in Illiquid Markets," NBER Working Paper No. 10411, April 2004.
35. A. Lynch and S. Tan, "Explaining the Magnitude of Liquidity Premia: The Roles of Return Predictability, Wealth Shocks and State-Dependent Transaction Costs," presented at Spring 2004 Asset Pricing Program Meeting.
36. A.W. Lo, H. Mamaysky, and J.Wang, "Asset Prices and Trading Volume Under Fixed Transactions Costs," NBER Working Paper No. 8311, May 2001, and Journal of Political Economy, 112, 5 (October 2004), pp. 1054-90.
37. A. W. Lo and J. Wang, "Trading Volume: Implications of An Intertemporal Capital Asset Pricing Model," NBER Working Paper No. 8565, October 2001.
38. G. Llorente, R. Michaely, G. Saar, and J. Wang, "Dynamic Volume-Return Relation of Individual Stocks," NBER Working Paper No. 8312, May 2001, and forthcoming, Review of Financial Studies.