Director

Sydney C. Ludvigson is the Julius Silver, Roslyn S. Silver, and Enid Silver Winslow Professor of Economics at New York University. Her research focuses on the interplay between asset markets and macroeconomic activity. She has been an NBER affiliate since 2003.
Featured Program Content

Property taxes represent the largest discretionary revenue source for local governments in the United States. Because these taxes are collected by...
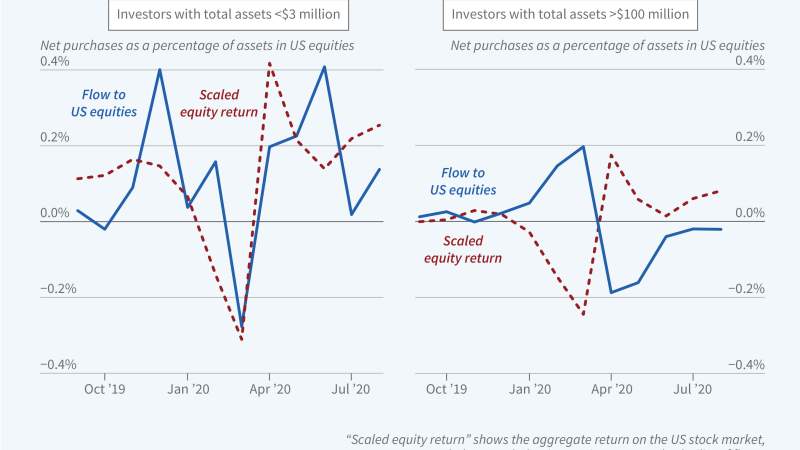
How investors adjust their portfolios in response to movements in asset prices and other shocks is a key input to asset pricing models, yet data limitations...

Endowments sustain the operations and activities of many nonprofit organizations, yet little is known about how they are invested or the returns that they earn...