LOGIT

Options     Examples     References

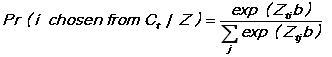
LOGIT is used to estimate a conditional and/or multinomial logit model. The explanatory variables in the model may vary across alternatives (choices) for each observation or they may be characteristics of the observation, or both. There is no limit on the number of alternatives.

LOGIT (CASE=var, COND, NCHOICE=n, NREC=var, SUFFIX=list, nonlinear options)

             <dependent variable> <independent variables> ;

             or

             <dependent variable> <conditional variables> | <multinomial(alternative) variables> ;

Usage

There are three types of logit model: those where the regressors are the same across all choices for each observations, i.e., they are characteristics of the chooser, those where the regressors are characteristics of the specific choice, and mixed models, which have regressors of both kinds. In the first case (multinomial logit), a separate coefficient for each regressor is estimated for all but one of the choices. In the second case (conditional logit), the regressors change across the choices, and a single coefficient is estimated for each set of regressors.

1. Binary or multinomial logit -- like OLSQ or PROBIT:

LOGIT dependent variable multinomial variables (chooser characteristics);

LOGIT Y C X1 X2 ... XK;

Y can be 0/1 or 1/2 or any integral values. If Y takes on more than 2 values, the model is multinomial logit. The names of the coefficients are determined by appending the values of Y for each choice to the names of the explanatory variables. The coefficients are normalized by setting the coefficients for the lowest choice to 0. If Y is 0/1, the coefficients C1, X11, X21,..., XK1 would be estimated, with C0, X10, X20,..., XK0 normalized to zero. If Y is 1/2/3, the coefficients C2, X12, X22,..., XK2 and C3, X13, X23,..., XK3 would be estimated, with C1, X11, X21,..., XK1 normalized to zero.

LOGIT (NCHOICE=2) Y C X1 X2 ... XK;

Including the NCHOICE option causes TSP to check the range of Y to make sure there are only 2 choices. The model estimated has K+1 coefficients and K+1 variables.

The multinomial logit procedure checks for "univariate complete and quasi-complete separation", which prevents identification of the coefficients.

2. Conditional logit:

LOGIT (COND,NCHOICE=n)

            <dependent variable> <conditional variables> | (<choice characteristics>);

For example,

LOGIT (COND,NCHOICE=2) Y X Z;

looks for the variables X1,X2,Z1,Z2 corresponding to the 2 choices. The coefficients X and Z would be estimated. C is not allowed as a conditional variable (since it does not vary across choices, it is not identified). For a choice-specific set of dummies, use C as a multinomial variable in mixed logit. In this case, the example shown becomes

LOGIT (COND,NCHOICE=2) Y X Z | C;

The CASE option allows you to use data organized with one choice per observation rather than with one case per observation. For example,

LOGIT (CASE=V) Y X Z ;

where the variable V is a case ID which is equal for adjacent observations which belong to the same case. In this case, the variable names X and Z are used directly (not X1,X2, etc.). There need not be an equal number of observations per case. Only the first Y for each case is examined for a valid choice number.

For datasets with multiple observations per case, you can also use

LOGIT (NREC=W) Y X Z;

W specifies the number of records per case and you do not need to supply an ID variable with the CASE option.

3. Mixed logit:

The general form of the command is now

LOGIT (COND,NCHOICE=n)

             <dependent variable> <conditional variables> | <multinomial variables> ;

For example,

LOGIT (COND,NCHOICE=3) Y ZA ZB | XA XB XC;

Y takes on the values 1,2, and 3. TSP looks for the conditional variables ZA1, ZA2, ZA3, ZB1, ZB2, ZB3 corresponding to the 3 choices. XA, XB, XC are the multinomial variables. The coefficients ZA, ZB, XA2, XB2, XC2,  XA3, XB3, XC3 would be estimated, with XA1, XB1, XC1 normalized to zero.

Output

The printed output of the LOGIT procedure is similar to that of the other nonlinear estimation procedures in TSP. A title is followed by a table of the frequency distribution of the choices. Then the starting values and iteration-by-iteration printout is printed; the amount is controlled by the PRINT and SILENT options. This is followed by a message indicating final convergence status, the value of the likelihood and a table of parameter estimates and their asymptotic standard errors and t-statistics. The variance-covariance matrix of the estimates is also printed if it has been unsuppressed. The @DPDX or @DPDZ matrices (described below) are printed unless they have been SUPRESed. The following are also stored in data storage:

Method

If C(t) is the choice set for the tth observations, and observation t chooses the ith alternative out of C(t), then the expression for the choice probability is

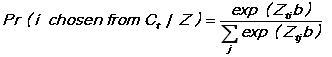
The likelihood function is

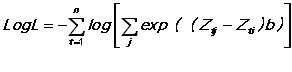
The coefficient vector to be estimated is b. If some of the Zs do not vary across the choices, these equations would apply to an expanded Z vector formed by taking the Kronecker product of the fixed Zs with an identity matrix of order of the number of choices (less one for a normalization). The actual implementation does not expand the Zs, but treats the conditional and multinomial variables differently to conserve space.

Newton's method is used to maximize this likelihood function with respect to the parameter vector b. The global concavity of the likelihood function makes estimates fairly straightforward to obtain with this method. Zero starting values are the default, unless @START is supplied. See the NONLINEAR section in this manual for more information about TSP's nonlinear optimization procedures in general.

The evaluation of the EXP() functions in the likelihood function and derivatives avoids floating overflows and zero divides. When these conditions occur, the appropriate limit is taken instead. This may result in some slight inaccuracy in the likelihood function, but it is certainly preferable to halting the estimation. Observations subject to these problems can be identified by exact 0 and 1 values in @FIT.

Before estimation, LOGIT checks for univariate complete and quasi-complete separation of the data and flags this condition. The model is not identified in this case, because one or more of the independent variables perfectly predict Y for some observations, and therefore their coefficients would slowly iterate to + or - infinity if estimation was allowed to proceed.

The scaled R-squared is a measure of goodness of fit relative to a model with just a constant term; it  replaced the Kullback-Leibler R-squared beginning with TSP 4.5 since it has somewhat better properties for discrete dependent variable problems. See the Estrella (1998) article.

Options

The standard options for nonlinear estimation are available: see the NONLINEAR section in this manual. Note that HITER=N,  HCOV=N are the defaults for the Hessian approximation and standard error computations. In addition, the following options are specifically for the LOGIT procedure:

CASE= case series for multiple observations per case. This variable holds a case identification which is equal for adjacent observations that belong to the same case. Note that any such variable may be used; it does not necessarily have to be the case identification.

COND/NOCOND for conditional or mixed models versus pure multinomial estimation (see the Usage section). If CASE= or NREC= is used, COND is assumed and need not be specified.

NCHOICE= number of choices can be supplied when the number is equal for all observations. The program then checks to make sure the data satisfy this constraint. This is not used with CASE= or NREC=, since then it is valid to take the first choice every time.

NREC= choice count series for multiple observations per case. This variable specifies the number of observations in each case. Usually the number is repeated in each observation, but only the count in the first observation for each case is used. You cannot say NREC=3, but you can say NCHOICE=3.

SUFFIX= a list of short names (suffixes) for the alternatives. These names are used  in 4 places: in the initial table of frequencies for the dependent variable, as coefficient names for multinomial variables, as labels for the probability derivatives dP/dZ, and as the suffixes for conditional variable names (when there is one observation per case). Note that SUFFIX does not imply COND.  

For example, assume that the dependent variable Y is coded 1,2,3.

LOGIT(COND,NCHOICE=3) Y XA XB;   

will use the conditional variables  XA1,XA2,XA3,XB1,XB2,XB3.

LOGIT(COND,NCHOICE=3,SUFFIX=(CAR,BUS,RT)) Y XA XB;  

will use the conditional variables  XACAR,XABUS,XART,XBCAR,XBBUS,XBRT.

The SUFFIX names need to be in the proper order, relative to the values of the dependent variable. In the above example, Y=1 is CAR, Y=2 is BUS, and Y=3 is RT. If some of the alternatives are never chosen, be sure to use SUFFIX= or NCHOICE= to ensure the full set of conditional variables is used (variables corresponding to all available alternatives).

Examples

NOSUPRES @DPDX ;   ? Allow the DPDX matrix to be printed.

LOGIT Y C X ;

LOGIT (COND, NCHOICE=3) Y XA XB ;

generates conditional variables XA1 XA2 XA3 and XB1 XB2 XB3, whereas

LOGIT (COND,NCHOICE=3,SUFFIX=(CAR,BUS,RT)) Y XA XB ;

generates conditional variables XACAR ,XABUS, XART and XBCAR ,XBBUS, XBRT. Note that the suffixes must be in the proper order (1,2,3) for correct interpretation of the output.

See the usage section for other examples of how to use this procedure.

References

Albert, A., and J.A. Anderson, "On the Existence of Maximum Likelihood Estimates in Logistic Regression Models," Biometrika 71 (1984).

Amemiya, Takeshi, Advanced Econometrics, Harvard University Press, 1985, Chapter 9.

Cameron, A. Colin, and Frank A. G. Windmeijer, “An R-squared Measure of Goodness of Fit for Some Common Nonlinear Regression Models,” Journal of Econometrics 77 (1997), pp.329-342.

Estrella, Arturo, “A New Measure of Fit for Equations with Dichotomous Dependent Variables,” Journal of Business and Economic Statistics, April 1998, pp. 198-205.

Hausman, Jerry A., and Daniel McFadden, “Specification Tests for the Multinomial Logit Model,” Econometrica 52 (1984): 1219-1240.

Maddala, G. S., Limited Dependent Variables and Qualitative Variables in Econometrics, Cambridge University Press, 1983, Chapters 2 and 3.

McFadden, Daniel, “Regression-Based Specification Tests for the Multinomial Logit Model,” Journal of Econometrics 34 (1987): 63-82.

McFadden, Daniel S., "Quantal Choice Analysis: A Survey," Annals of Economic and Social Measurement, 5 (1976), pp. 363-390.

McFadden, Daniel S., "Conditional Logit Analysis of Qualitative Choice Behavior," in Zarembka, P., ed., Frontiers in Econometrics, Academic Press, 1973.

Nerlove, Marc and S. James Press, "Univariate and Multivariate Loglinear and Logistic Models," Rand Report No. R-1306-EDA/NIH, 1973.

Train, Kenneth, Quantitative Choice Analysis, The MIT Press, Cambridge, MA, 1986.