PROBIT

Options     Example     References

PROBIT obtains estimates of the linear probit model, where the dependent variable takes on only two values. Options allow you to obtain and save the inverse Mills ratio as a series so that the sample selection correction due to Heckman can be estimated (also see the SAMPSEL command).

PROBIT (FEI,FEPRINT,MILLS=<name for output inverse Mills ratio>,

              NHERMITE=<number of points for hermite quadrature>,REI,nonlinear options)

              <dependent variable> <list of independent variables> ;

Usage

The basic PROBIT statement is like the OLSQ statement: first list the dependent variable and then the independent variables. If you wish to have an intercept term in the regression (usually recommended), include the special variable C or CONSTANT in your list of independent variables. You may have as many independent variables as you like subject to the overall limits on the number of arguments per statement and the amount of working space, as well as the number of data observations you have available.

The observations over which the regression is computed are determined by the current sample. If any of the observations have missing values within the current sample, PROBIT will print a warning message and will drop those observations. PROBIT also checks for complete or quasi-complete sample separation by one of the right hand side variables; such models are not identified.

The list of independent variables on the PROBIT command may include variables with explicit lags and leads as well as PDL (Polynomial Distributed Lag) variables. These distributed lag variables are a way to reduce the number of free coefficients when entering a large number of lagged variables in a regression by imposing smoothness on the coefficients. See the PDL section for a description of how to specify such variables.

The dependent variable need not be a strictly zero/one variable. Positive values are treated as one and zero or negative values are treated as zero.

The FEI and REI options compute estimates for models with fixed and random effects for individuals respectively. FREQ (PANEL) must be in effect. For fixed effects, a very efficient algorithm is used, so large unbalanced panels can easily be handled. The FEPRINT option prints a table of the effects, their standard errors, and t-statistics. Individuals that have dependent variable values that are all zero or all one are allowed, although their data is not informative for the slopes. The fixed effects for such individuals will be either a very large negative number (in the case of zero) or a very large positive number (in the case of one). These values yield the correct probability for these observations (zero or one). Note that this estimator has a finite-T  bias, so the number of time periods per individual should not be too small. The random effects model is estimated by maximum likelihood; see the method section below for details.

Output

The output of PROBIT begins with an equation title and the name of the dependent variable. Starting values and diagnostic output from the iterations will be printed. Final convergence status is printed.

This is followed by the mean of the dependent variable, number of positive observations, sum of squared residuals, R-squared, and a table of right hand side variable names, estimated coefficients, standard errors and associated t-statistics.

PROBIT also stores some of these results in data storage for later use. The table below lists the results available after a PROBIT command.

If the regression includes a PDL variable, the following will also be stored:

Method

PROBIT uses analytic first and second derivatives to obtain maximum likelihood estimates via the Newton-Raphson algorithm. This algorithm usually converges fairly quickly. TSP uses zeros for starting parameter values, unless @START is used to override this (see the NONLINEAR entry). As in other regression procedures in TSP, estimation is done using a generalized inverse in the case of multicollinearity of the independent variables.

The numerical implementation involves evaluating the normal density and cumulative normal distribution functions. The cumulative normal distribution function is computed from an asymptotic expansion, since it has no closed form. See the reference under the CDF command for the actual method used to evaluate CNORM(). The ratio of the density to the distribution function is also known as the inverse Mills ratio. This is used in the derivatives and with the MILLS= option.

@MILLS is actually the expectation of the structural residual, where the model is given by

@MILLS is the value of the following two expressions, depending on whether D=0 or 1:

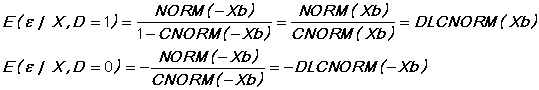
where NORM is the normal density, CNORM is the cumulative normal and DLCNORM is the derivative of the log cumulative normal with respect to its argument. Before estimation, PROBIT checks for univariate complete and quasi-complete separation of the data and flags this condition. The model is not identified in this case, because one or more of the independent variables perfectly predict the dependent variable for some of the observations, and therefore their coefficients would slowly iterate to plus or minus infinity if estimation was allowed to proceed.

The scaled R-squared is a measure of goodness of fit relative to a model with just a constant term; it  replaced the Kullback-Leibler R-squared beginning with TSP 4.5 since it has somewhat better properties for discrete dependent variable problems. See the Estrella (1998) article.

The Probit random effects model estimated is the following:

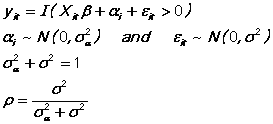
This normalization means that the slope estimates are normalized the same way as the results from the usual Probit command. The parameter RHO is estimated and corresponds to the share of the variance that is within individual. The likelihood function involves computing a multivariate integral and this is done with Hermite quadrature, using a default 20 points; when RHO is high, it may be necessary to increase this using the NHERMITE option.

Options

FEI/NOFEI specifies that the fixed effects Probit model should be computed. FREQ (PANEL) must be in effect.

FEPRINT/NOFEPRIN  specifies whether the estimated effects and their standard errors should be printed.

MILLS= the name of a series used to store the inverse Mills ratio series evaluated at the estimated parameters. The default is @MILLS.

NHERMITE= number of points for the Hermite quadrature in computing the integral for the random effects Probit model. The default is 20. The value set is retained throughout the TSP run.

REI/NOREI specifies that the random effects Probit model should be computed. FREQ (PANEL) must be in effect.

The usual nonlinear estimation options can be used. See the NONLINEAR entry.

Examples

Standard probit model:

PROBIT MOVE C WAGE1 WAGE2 COST1 COST2;

Heckman sample selection model (see the SAMPSEL command for ML estimation of this model):

PROBIT (MILLS=RMILL) WORK C OCC1 OCC2 TENURE MSTAT AGE;

SELECT WORK;

OLSQ LWAGE C SCHOOL EXPER IQ UNION OCC1 OCC2 RMILL;

Computing fitted probabilities and inverse Mills ratios explicitly:

PROBIT MOVE C WAGE1 WAGE2 COST1 COST2;

FORCST XB;

MOVEP = CNORM(XB);

MILLSR = MOVE * DLCNORM(XB) + (1-MOVE) * (-DLCNORM(-XB));

References

Amemiya, Takeshi, "Qualitative Response Models: A Survey," Journal of Economic Literature 19, December 1981, pp. 1483-1536.

Cameron, A. Colin, and Frank A. G. Windmeijer, “An R-squared Measure of Goodness of Fit for Some Common Nonlinear Regression Models,” Journal of Econometrics 77 (1997), pp.329-342.

Estrella, Arturo, “A New Measure of Fit for Equations with Dichotomous Dependent Variables,” Journal of Business and Economic Statistics, April 1998, pp. 198-205.

Maddala, G. S., Limited-dependent and Qualitative Variables in Econometrics, Cambridge University Press, New York, 1983, pp. 22-27, 221-223, 231-234, 257-259, 365.