OLSQ

Options     Examples     References

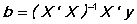
OLSQ is the basic regression procedure in TSP. It obtains ordinary least squares estimates of the coefficients of a regression of the dependent variable on a set of independent variables. Options allow you to obtain weighted least squares estimates to correct for heteroskedasticity, or to obtain standard errors which are robust in the presence of heteroskedasticity of the disturbances (see the GMM command for robustness to autocorrelation).

OLSQ (HCTYPE=<robust SE type>, HI, NORM or UNNORM, ROBUSTSE, SILENT, TERSE,

           WEIGHT=<name of weighting variable>, WTYPE=weight type)

           <dependent variable> <list of independent variables> ;

Usage

In the basic OLSQ statement, you list the dependent variable and then the independent variables in the equation. To have an intercept term in the regression, include the special variable C or CONSTANT in the list of independent variables. The number of independent variables is limited by the overall limits on the number of arguments per statement and the amount of working space; obviously, it is also limited by the number of data observations available.

The observations over which the regression is computed are determined by the current sample. If any observations have missing values within the current sample, they are dropped from the sample, and a warning message is printed for each series with missing values. The number of observations remaining is printed with the regression output. @RES and @FIT will have missing values in this case, and the Durbin-Watson will be adjusted for the sample gaps.

The list of independent variables on the OLSQ command may include variables with explicit lags and leads as well as PDL (Polynomial Distributed Lag) variables. These PDL variables are a way to reduce the number of free coefficients when you are entering a large number of lagged variables in a regression by imposing smoothness on the coefficients. See the PDL section for a description of how to specify a PDL variable.

Output

The output of OLSQ begins with an equation title and the name of the dependent variable. This is followed by statistics on goodness-of-fit: the sum of squared residuals, the standard error of the regression, the R-squared, the Durbin-Watson statistic for auto correlation of the residuals, a Lagrange multiplier test for heteroskedasticity, the Jarque-Bera test for normality, and an F-statistic for the hypothesis that all coefficients in the regression except the constant are zero. If there is no constant in the regression and the mean was not removed from the dependent variable prior to the regression, the F-statistic may be meaningless. See the REGOPT command for a large variety of additional regression diagnostics.

A table of right hand side variable names, estimated coefficients, standard errors and associated t-statistics follows. Use

REGOPT (PVPRINT) T;

to turn on the printing of P-values and stars for significance of the t-statistics. The variance-covariance and correlation matrices are printed next if they have been selected with the REGOPT command.

If there are lagged dependent variables on the right hand side, the regular Durbin-Watson statistic is biased, so an alternative test for serial correlation is computed. The statistic is computed by including the lagged residual with the right hand side variables in an auxiliary regression (with the residual as the dependent variable), and testing the lagged residual's coefficient for significance. See the Durbin reference for details; this method is very similar to the method used for correcting the standard errors for AR1 regression coefficients in the same lagged dependent variables case. This statistic is more general than "Durbin's h" statistic since it applies in cases of several lagged dependent variables. It is not computed if there is a WEIGHT or gaps in the SMPL, and the presence of lagged dependent variables is not detected if they are computed with GENR (instead of being specified with an explicit lag like OLSQ Y C X Y(-1); or in a PDL).

If the PLOTS option is on, TSP prints and plots the actual and fitted values of the dependent variable and the residuals. OLSQ also stores most of these results in data storage for your later use. The table below lists the results available:

If the regression includes a PDL or SDL variable, the following will also be stored:

REGOPT (NOPRINT) LAGF;

will turn off the lag plot for PDL variables.

Method

OLSQ computes the matrix equation:

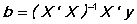
where X is the matrix of independent variables and y is the vector of independent variables. The method used to compute this regression (and all the other regression-type estimates in TSP) is a very accurate one, which involves applying an orthonormalizing transformation to the X matrix before computation of the inner products and inverse, and then untransforming the result (see ORTHON in this manual). See OPTIONS FAST; to compute faster and slightly less accurate regressions (without orthonormalization).

OLSQ has been tested using the data of Longley on everything from an IBM 370 to a modern Pentium computer; it gives accurate results to six digits when the data is single precision. For the artificial problem suggested by Lauchli (see the Wampler article), OLSQ gives correct results for the coefficients to about five places, until epsilon becomes so small that the regression is not computable. Before this happens, OLSQ detects the fact that it cannot compute the regression accurately and drops one of the variables by setting its coefficient to zero and printing a warning. The results for these special regressions become more accurate when OPTIONS DOUBLE ; is in effect, because these data have an unusually high number of significant digits. See the Benchmarks section of the TSP web page for more information on regression accuracy with Longley and other standard regression datasets.

Options

HCTYPE=  the type of heteroskedastic-consistent standard errors to compute (between 0 and 3, with a default of 2. This option implies ROBUSTSE. In general, the robust estimate of the variance-covariance matrix has the form:

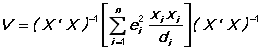
The option HCTYPE specifies the formula used for d(i):

where h(i) is the diagonal of the "hat matrix" (defined below). If 1-h(i) is zero for some i, (T-k)/T is substituted. Both HCTYPE=2 and HCTYPE=3 have good finite sample properties. See Davidson and MacKinnon, pp. 552-556 for details.

HI/NOHI specifies whether the diagonal of the "hat matrix" is stored in the series @HI. The hat matrix is defined as

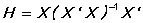
This is useful for detecting "influential" observations (data errors, outliers, etc.). For example,

SELECT @HI > 2*@NCOEF/@NOB;

identifies the influential observations. (See the Belsley, Kuh, and Welsch or Krasker, Kuh, and Welsch references).

NORM/UNNORM tells whether the weights are to be normalized so that they sum to the number of observations. This has no effect on the coefficient estimates and most of the statistics, but it makes the magnitude of the unweighted and weighted data the same, on average, which may help in interpreting the results. The coefficient standard errors and t-statistics are affected. NORM has no effect if the WEIGHT option has not been specified.

ROBUSTSE/NOROBUST causes the variance of the coefficient estimates, the standard errors, and associated t-statistics to be computed using the formulas suggested by White, among others. These estimates of the variance are consistent even when the disturbances are not homoskedastic, and when their variances are correlated with the independent variables in the model. They are not consistent when the disturbances are not independent, however. See the Davidson and MacKinnon reference. See the HCTYPE= option for the exact formulas.

SILENT/NOSILENT suppresses all output. The results are stored.

TERSE/NOTERSE suppresses all regression output except for the log likelihood and the table of coefficients and standard errors.

WEIGHT= the name of a series used to weight the observations. The data are multiplied by the square roots of the normalized weighting series before the regression is computed (see NORM above). The series will be proportional to the inverses of the variances of the residuals. If the weight is zero for a particular observation, that observation is not included in the computations nor is it counted in determining degrees of freedom.

WTYPE= HET or REPEAT, the weight type. The default is REPEAT, where the weight is a repeat count (it multiplies the likelihood function directly). This is used for grouped data and is consistent with the UNNORM option. WTYPE=HET means the weight is for heteroskedasticity only (it enters the likelihood function only through F). The only difference between these two options in the regression output is the value of the log likelihood function (all the coefficients, standard errors, etc. are identical). With WTYPE=HET, the log likelihood includes the sum of the log weights; the default WTYPE=REPEAT does not include this.  

Examples

This example estimates the consumption function for the illustrative model:

OLSQ CONS,C,GNP ;

Using population as weights, the next example regresses the fraction of young people living alone on other demographic characteristics across states. Since the regression is in terms of per capita figures, the variance of the disturbances is proportional to the inverse of population.

OLSQ (WEIGHT=POP) YOUNG,C,RSALE,URBAN,CATHOLIC ;

Other examples of the OLSQ command:

OLSQ (ROBUSTSE) LOGP C LOGP(-1) LOGR ;

OLSQ TBILL C RATE(4,12,FAR) ;

References

Belsley, David A., Kuh, Edwin, and Welsch, Roy E., Regression Diagnostics: Identifying Influential Data and Sources of Collinearity, John Wiley & Sons, New York, 1980, pp. 11-18.

Davidson, Russell, and James G. MacKinnon, Estimation and Inference in Econometrics, Oxford University Press, New York, 1993, pp.552-556.

Durbin, J., "Testing for Serial Correlation in Least-Squares Regression When Some of the Regressors are Lagged Dependent Variables," Econometrica 38 (1970), p. 410-421.

Durbin, J., and G.S. Watson, “Testing for Serial Correlation in Least Squares Regression,” Biometrika 38 (1951), pp. 159-177.

Judge et al, The Theory and Practice of Econometrics, John Wiley & Sons, New York, 1981, pp. 11-18, 126-144.

Krasker, William S., Kuh, Edwin, and Welsch, Roy E., "Estimation for Dirty Data and Flawed Models," Handbook of Econometrics, Volume I, Griliches and Intrilligator (eds.), North-Holland Publishing Co., New York, 1983, pp. 660-664.

Longley, James W., "An Appraisal of Least Squares Programs for the Electronic Computer from the Point of View of the User," JASA, 1967, pp. 818-841.

MacKinnon, James G., and Halbert White, "Some heteroskedasticity consistent covariance matrix estimators with improved finite sample properties," Journal of Econometrics 29, pp.305-325.

Maddala, G. S., Econometrics, McGraw Hill Book Company, New York, 1977, pp. 104-127, 257-268.

Pindyck, Robert S., and Daniel L. Rubinfeld, Econometric Models and Economic Forecasts, McGraw Hill Book Company, New York, 1976, Chapter 2,3,4.

Wampler, Roy H., "Test Procedures and Test Problems for Least Squares Algorithms," Journal of Econometrics, 12, pp 3-21.