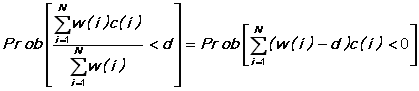
CDF calculates and prints tail probabilities (P-values or significance levels) or critical values for several cumulative distribution functions. This is useful for hypothesis testing.
CDF (BIVNORM or CHISQ or DICKEYF or F or NORMAL or T or WTDCHI,
CONSTANT, DF=<degrees of freedom for CHISQ or T>,
DF1=<numerator degrees of freedom for F>,
DF2=<denominator degrees of freedom for F>,
EIGVAL=<vector of eigenvalues for WTDCHI>,
LOWTAIL or UPTAIL or TWOTAIL, INVERSE,
NLAGS=<number of lags for augmented Dickey-Fuller test>,
NOB=<number of observations for unit root or cointegration test>,
NVAR=<number of variables for cointegration test>,
PRINT, RHO=<correlation coefficient for BIVNORM>,
TREND, TSQ)
<test statistic> [<significance level>] ;
or
<significance level> [<critical value>] ; (for INVERSE)
or
<x value> <y value> [<significance level>]; (for BIVNORM)
Usage
CDF followed by the value of a scalar test statistic is the simplest form of the command. In this case, a two-tailed probability for the normal distribution will be calculated and printed. If the INVERSE option is used, the first argument must be a probability level; a critical value will be calculated. Arguments need not be scalars; they can be series or matrices. Distributions other than the normal and/or a choice of tail areas may be selected through the options. For hypothesis testing using a wide variety of regression diagnostics, see the REGOPT (PVPRINT) command.
Output
If the PRINT option is on, the input and output values will be printed, along with the degrees of freedom. If a second argument is supplied, it will be filled with the output values and stored (see examples 4 and 6). Input and output arguments may be any numeric TSP variables.
Method
BIVNORM: ACM Algorithm 462. Inverse is not supplied because it is not unique unless x or y is known, etc.
CHISQ: DCDFLIB method: Abramovitz-Stegun formula 26.4.19 converts it to Incomplete Gamma, and then use DiDinato and Morris (1986). Inverse by iteration (trying values of x to yield p -- faster methods are also known). Non-integer degrees of freedom are allowed, and can be used to compute the incomplete gamma function.
F and T: DCDFLIB method: Abramovitz-Stegun formula 26.6.2 converts it to Incomplete Beta, and then use DiDinato and Morris (1993), i.e. ACM Algorithm 708. Inverse by iteration. Non-integer degrees of freedom for F are allowed, and can be used to compute the incomplete beta function.
NORMAL: ACM Algorithm 304, with quadratic approximation for E<-37.5. Inverse: Applied Statistics Algorithm AS241, from StatLib.
DICKEYF: Asymptotic values from Tables 3 and 4 in MacKinnon (1994). Finite sample critical values from Cheung and Lai (1995) [augmented Dickey-Fuller] or MacKinnon (1991) [Engle-Granger]. To convert these to finite sample P-values, a logistic interpolation is used with the .05 size and either the .01 or .10 size (whichever is closer to the observed test statistic). Such interpolated P-values are fine for testing at the .01, .05, or .10 sizes, but would be highly speculative outside this range.
WTDCHI: If w(i) are the eigenvalues (supplied by the option EIGVAL), c(i) are chi-squared(1) variables, and d is the test statistic (supplied as an argument), WTDCHI computes the following probability:
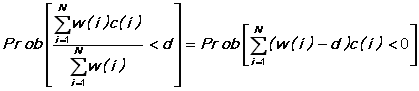
This is useful for computing P-values for the Durbin-Watson statistic, other ratios of quadratic forms in normal variables, and certain non-nested tests (for example, Vuong (1989) suggests likelihood ratio tests for nonnested hypotheses). The Pan method is used when the number of eigenvalues is less than 90; otherwise the Imhoff method is used. If the absolute values of the smallest eigenvalues are less than 1D-12, they are not used; otherwise duplicate eigenvalues are not checked for. The inverse of this distribution is not implemented.
BIVNORM/CHISQ/DICKEYF/F/NORMAL/T/WTDCHI specifies the bivariate normal, chi-squared, Dickey-Fuller, F, standard normal, student's t, and weighted chi-squared distributions, respectively.
CONSTANT/NOCONST specifies whether a constant term (C) was included in the regression for Dickey-Fuller. NOCONST is only valid for NVAR=1.
DF= the degrees of freedom for the chi-squared or student's t distribution, or the number of observations for Dickey-Fuller (also see the NOB= option for Dickey-Fuller). Non-integers allowed for the chi-squared.
DF1= the numerator degrees of freedom for the F distribution (can be non-integer).
DF2= the denominator degrees of freedom for the F distribution (can be non-integer).
EIGVAL= vector of eigenvalues for the weighted chi-squared distribution.
INVERSE/NOINVERSE specifies the inverse distribution function (input is significance level, output is critical value). Normally the input is a test statistic and the output is a significance level. INVERSE is not defined for bivariate normal.
LOWTAIL/TWOTAIL/UPTAIL specifies the area of integration for the density function. TWOTAIL is the default for most symmetric distributions (normal and t), UPTAIL is the default for chi-squared and F, and LOWTAIL is the default for bivariate normal and Dickey-Fuller. TWOTAIL is not defined for bivariate normal.
NLAGS= the number of lagged differences in the augmented Dickey-Fuller test. This number is used to compute the approximate finite sample P-value or critical value. The default is zero (assume an unaugmented test). The NOB= option must also be specified for the finite sample value.
NOB= the number of observations for the augmented Dickey-Fuller or Engle-Granger tests. This number is used to compute the approximate finite sample P-value or critical value. The default is zero (to compute asymptotic instead of finite sample value).
NVAR= the number of variables for an Engle-Granger/Dickey-Fuller cointegration test. The default is 1 (plain unit root test), and the maximum is 6.
RHO= the correlation coefficient for the bivariate normal distribution.
TREND/NOTREND specifies whether a trend term (1,2,...,T) was included in the regression for Dickey-Fuller.
TSQ/NOTSQ specifies whether a squared trend term (1,4,9,...) was included in the regression for Dickey-Fuller.
PRINT/NOPRINT turns on printing of results. PRINT is true by default if there is no output specified.
To compute the significance level of a Hausman test statistic with 5 degrees of freedom:
CDF (CHISQ,DF=5) HAUS;
produces the output:
CHISQ(5) Test Statistic: 7.235999 , Upper tail area: .20367
Significance level of the test for AR(1) with lagged dependent variable(s):
CDF @DHALT;
or REGOPT (PVPRINT) DHALT; before the regression is run
Two-tailed critical value for the normal distribution:
CDF (INV) .05;
produces the output:
NORMAL Critical value: 1.959964 , Two-tailed area: .05000
Several critical values for the normal distribution:
READ PX; .1 .05 .01 ;
CDF(INV,NORM) PX CRIT;
PRINT PX,CRIT;
F critical values:
CDF(INV,F,DF1=3,DF2=10) .05;
produces the output:
F(3,10) Critical value: 3.708265 , Upper tail area: .05000
Bivariate normal:
CDF(BIVNORM,RHO=.5,PRINT) -1 -2 PBIV;
produces the output:
BIVNORM Test Statistic: -1.0000 , -2.0000 , Lower tail area: .01327
Dickey-Fuller unit root test:
TREND TIME;
SMPL 2,50;
DY = Y-Y(-1);
OLSQ DY TIME C Y(-1);
CDF(DICKEYF) @T(3);
? The above is equivalent to the following:
UNIT(MAXLAG=0,NOWS) Y;
Augmented Dickey-Fuller unit root test, with finite sample P-value:
TREND TIME;
SMPL 2,50;
DY = Y-Y(-1);
SMPL 5,50;
OLSQ DY TIME C Y(-1) DY(-1)-DY(-3);
CDF(DICKEYF,NOB=@NOB,NLAGS=3) @T(3);
? The above is equivalent to the following:
UNIT(MAXLAG=3,NOWS,FINITE) Y;
Engle-Granger cointegration test:
TREND TIME;
OLSQ Y1 TIME C Y2 Y3 Y4; EGTEST;
OLSQ Y2 TIME C Y1 Y3 Y4; EGTEST;
OLSQ Y3 TIME C Y1 Y2 Y4; EGTEST;
OLSQ Y4 TIME C Y1 Y2 Y3; EGTEST;
PROC EGTEST;
SMPL 2,50;
DU = @RES-@RES(-1);
OLSQ DU @RES(-1);
CDF(DICKEYF,NVAR=4) @T;
SMPL 1,50;
ENDPROC;
? The above is equivalent to the following:
COINT (NOUNIT,MAXLAG=0,ALLORD) Y1-Y4;
Verify critical values for Durbin-Watson statistic, for regression with 10 observations and 2 RHS variables:
SMPL 1,10; OLSQ Y C X1;
SET PI = 4*ATAN(1); SET F = PI/(2*@NOB); TREND I;
EIGB = 4*SIN(I*F)**2;
SELECT I <= (@NOB-@NCOEF); ? use largest eigenvalues for dL
CDF (WTDCHI,EIG=EIGB) .879; ? dL for 5% (n=10, k==1)
SELECT (@NCOEF <= I) & (I <= (@NOB-1)); ? use smallest eigenvalues for dU
MMAKE dU 1.320 1.165 1.001; ? dU for 5%, 2.5%, 1% (n=10, k==1)
CDF (WTDCHI,EIG=EIGB,PRINT) dU;
Reproduce exact P-value for Durbin-Watson statistic (this can be done automatically using REGOPT):
SMPL 1,10; ? data from Judge, et al (1988) example: DW = 1.037, P-value = .0286
READ Y X1; 4 2 7 4 7.5 6 4 3 2 1 3 2 5 3 4.5 4 7.5 8 5 6 ;
REGOPT (DWPVAL=EXACT);
OLSQ Y C X1;
MMAKE X @RNMS;
MAT XPXI = (X=X)@;
TREND OBS; SELECT OBS > 1;
DC = 0; DX1 = X1 - X1(-1);
MMAKE DX DC DX1;
MMAKE BVEC 2 -1; MFORM(BAND,NROW=@NOB) DDP = BVEC;
MAT DMDP = DDP - DX*XPXI*DX=;
? Eigenvalues of DMD= = D*D= - DX*(X=X)@(DX)=
? (same as nonzero eigenvalues of MA, because A = D=D)
MAT ED = EIGVAL(DMDP);
CDF (WTDCHI,EIG=ED) @DW;
Cheung, Yin-Wong, and Lai, Kon S., "Lag Order and Critical Values of the Augmented Dickey-Fuller Test," Journal of Business and Economic Statistics, July 1995, pp. 277-280.
ACM, Collected Algorithms, New York, 1980.
Brown, Barry W. DCDFLIB. http://odin.mdacc.tmc.edu , downloaded v1.1, 4/1998.
DiDinato, A.R. and Morris, Alfred H. Jr., "Computation of the Incomplete Gamma Function Ratios and Their Inverse," ACM Transactions on Mathematical Software 12, 1986, pp. 377-393.
DiDinato, A.R. and Morris, Alfred H. Jr., "Algorithm 708: Significant Digit Computation of the Incomplete Beta Function Ratios," ACM Transactions on Mathematical Software 18, 1993, pp. 360-373.
Engle, R.F., and Granger, C.W.J., "Co-integration and Error Correction: Representation, Estimation, and Testing," Econometrica 55 (1987), pp. 251-276.
Imhoff, P.J., "Computing the Distribution of Quadratic Forms in Normal Variables," Biometrika 48, 1961, pp. 419-426.
Inverse Normal Computation, Algorithm AS 241, Applied Statistics 37 (1988), Royal Statistical Society.
Judge, George G., Hill, R. Carter, Griffiths, William E., Lutkepohl, Helmut, and Lee, Tsoung-Chao, Introduction to the Theory and Practice of Econometrics, second edition, Wiley, New York, 1988, pp. 394-400.
MacKinnon, James G., "Critical Values for Cointegration Tests,"in Long-Run Economic Relationships: Readings in Cointegration, eds. R.F.Engle and C.W.J.Granger, New York: Oxford University Press, 1991, pp. 266-276.
MacKinnon, James G., "Approximate Asymptotic Distribution Functions for Unit-Root and Cointegration Tests," Journal of Business and Economic Statistics, April 1994, pp.167-176.
Pan, Jie-Jian, "Distribution of Noncircular Correlation Coefficients," Selected Transactions in Mathematical Statistics and Probability, 1968, pp. 281-291.
StatLib. http://lib.stat.cmu.edu/apstat/
Vuong, Quang H., "Likelihood Ratio Tests for Model Selection and Non-Nested Hypotheses," Econometrica 57, 1989, pp. 307-334.