REGOPT controls the calculation and output of the regression diagnostics for OLSQ and some output of other commands. It replaces the old SUPRES and NOSUPRES commands.
REGOPT (BPLIST=<list of variables>, CALC, CHOWDATE=<date for splitting sample>,
DWPVALUE=type, LMLAGS=<# of lags for LMAR test>,
PRINT, PVCALC, PVPRINT, QLAGS=<# of Q-statistics>, RESETORD=value,
SHORTLAB, STAR1=<value for *>, STAR2=<value for **>, STARS)
list of output names or keywords ;
Usage
OLSQ can produce a massive number of diagnostics. REGOPT provides the user with extensive customization of this output, so that irrelevant diagnostics do not crowd relevant ones or require extensive time to calculate. The [PV]CALC and [PV]PRINT options are used along with a list of the diagnostic codes (@names) that one wishes to control. The keywords AUTO, HET, REGOUT, and ALL may also be used to control groups of diagnostics (instead of listing all the names). Other options (such as BPLIST and LMLAGS) control individual diagnostics that have no clear default. OPTIONS LIMCOL= and SIGNIF= also control the display. Note that "robust" diagnostics are available with the HI option in OLSQ.
Output
The following three examples illustrate the range of output available.
Three examples of controlling regression output with REGOPT
The data for these examples is a regression squared on time:
options crt; smpl 1,10; trend t; t2 = t*t;
Example 1: default option
olsq t2 c t; ? default
Equation 1
============
Method of estimation = Ordinary Least Squares
Dependent variable: T2
Current sample: 1 to 10
Number of observations: 10
Mean of dep. var. = 38.5000 LM het. test = .391605 [.531]
Std. dev. of dep. var. = 34.1736 Durbin-Watson = .454545 [<.012]
Sum of squared residuals = 528.000 Jarque-Bera test = 1.01479 [.602]
Variance of residuals = 66.0000 Ramsey's RESET2 = .850706E+38 [.000]
Std. error of regression = 8.12404 F (zero slopes) = 151.250 [.000]
R-squared = .949765 Schwarz B.I.C. = 36.3245
Adjusted R-squared = .943485 Log likelihood = -34.0219
Estimated Standard
Variable Coefficient Error t-statistic P-value
C -22.0000 5.54977 -3.96412 [.004]
T 11.0000 .894427 12.2984 [.000]
Example 2: "short label" output
regopt(shortlab);
olsq t2 c t;
Equation 2
============
Method of estimation = Ordinary Least Squares
Dependent variable: T2
Current sample: 1 to 10
Number of observations: 10
YMEAN 38.5000 S 8.12404 DW .454545 [<.012] SBIC 36.3245
SDEV 34.1736 RSQ .949765 JB 1.01479 [.602] LOGL -34.0219
SSR 528.000 ARSQ .943485 RESET2 .850706E+38 [.000]
S2 66.0000 LMHET .391605 [.531] FST 151.250 [.000]
Estimated Standard
Variable Coefficient Error t-statistic P-value
C -22.0000 5.54977 -3.96412 [.004]
T 11.0000 .894427 12.2984 [.000]
Example 3: maximal output
regopt (pvprint,stars,bplist=(c,t),lmlags=2,qlags=2,noshort) all;
options signif=8; ? increase width of displayed numbers
? maximal output except for DH and DHALT(require lagged dependent var.)
olsq t2 c t;
Equation 3
============
Method of estimation = Ordinary Least Squares
Dependent variable: T2
Current sample: 1 to 10
Number of observations: 10
Mean of dep. var. = 38.5000000
Std. dev. of dep. var. = 34.1735765
Sum of squared residuals = 528.000000
Variance of residuals = 66.0000000
Std. error of regression = 8.12403840
R-squared = .949764521
Adjusted R-squared = .943485086
LM het. test = .391604968 [.531]
Durbin-Watson = .454545455 * [<.012]
Breusch/Godfrey LM: AR/MA1 = .850705917E+38 ** [.000]
Breusch/Godfrey LM: AR/MA2 = .850705917E+38 ** [.000]
Ljung-Box Q-statistic1 = 3.33333333 [.068]
Ljung-Box Q-statistic2 = 3.38842975 [.184]
ARCH test = .258229904 [.611]
CuSum test = 1.26364964 ** [.003]
CuSumSq test = .465909091 [.051]
Chow test = 53.5714286 ** [.000]
Chow het. rob. test = 53.5714286 ** [.000]
LR het. test (w/ Chow) = 26.4920970 ** [.000]
White het. test = 3.38983051 [.184]
Breusch-Pagan het. test = 1.74908036 [.186]
Jarque-Bera test = 1.01478803 [.602]
Shapiro-Wilk test = .869383609 [.098]
Ramsey's RESET2 = .850705917E+38 ** [.000]
F (zero slopes) = 151.250000 ** [.000]
Schwarz B.I.C. = 36.3245264
Akaike Information Crit. = 36.0219413
Log likelihood = -34.0219413
Estimated Standard
Variable Coefficient Error t-statistic P-value
C -22.0000000 5.54977477 -3.96412484 ** [.004]
T 11.0000000 .894427191 12.2983739 ** [.000]
Variance Covariance of estimated coefficients
C T
C 30.80000000
T -4.40000000 0.80000000
Correlation matrix of estimated coefficients
C T
C 1.0000000
T -0.88640526 1.0000000
ID ACTUAL(*) FITTED(+) RESIDUAL(0)
0
1 1.0000 -11.0000 + * 12.0000 + | + 0
2 4.0000 0.0000 +* 4.0000 + | 0+
3 9.0000 11.0000 + -2.0000 + 0| +
4 16.0000 22.0000 *+ -6.0000 0 | +
5 25.0000 33.0000 * + -8.0000 0+ | +
6 36.0000 44.0000 * + -8.0000 0+ | +
7 49.0000 55.0000 *+ -6.0000 0 | +
8 64.0000 66.0000 + -2.0000 + 0| +
9 81.0000 77.0000 +* 4.0000 + | 0+
10 100.0000 88.0000 + * 12.0000 + | + 0
CUSUM PLOT
***** ****
CUSUM PLOTTED WITH C
UPPER BOUND (5%) PLOTTED WITH U
LOWER BOUND (5%) PLOTTED WITH L
MINIMUM MAXIMUM
-8.04319191 10.72242260
|-+--------------------0----------------------------+-|
3 | L |C U |
4 | L | C U |
5 | L | C U |
6 | L | C U |
7 | L | C U |
8 | L | C U |
9 | L | UC |
10 | L | U C |
|-+--------------------0----------------------------+-|
-8.04319191 10.72242260
MINIMUM MAXIMUM
CUSUMSQ PLOT
******* ****
CUSUMSQ PLOTTED WITH C
MEAN PLOTTED WITH M
UPPER BOUND (5%) PLOTTED WITH U
LOWER BOUND (5%) PLOTTED WITH L
MINIMUM MAXIMUM
0.00000000 1.00000000
|-+-------------------------------------------------+-|
3 | 2 M U | CL
4 | 2 M U | CL
5 | LC M U |
6 | L C M U |
7 | 2 M U | CL
8 | L C M U |
9 | L C M U |
10 | L 3 | CMU
|-+-------------------------------------------------+-|
0.00000000 1.00000000
MINIMUM MAXIMUM
show scalar; ? list of scalar results showing @names and % names
Class Name Description
----- ---- -----------
SCALAR @NOB constant 10.00000000
@FREQ constant 0.00000000
@YMEAN constant 38.50000000
@SDEV constant 34.17357654
@SSR constant 528.00000000
@S2 constant 66.00000000
@S constant 8.12403840
@RSQ constant 0.94976452
@ARSQ constant 0.94348509
@LMHET constant 0.39160497
%LMHET constant 0.53145697
@DW constant 0.45454545
%DW constant 0.012096704
@JB constant 1.01478803
%JB constant 0.60206250
@RESET2 constant 8.5070592D+37
%RESET2 constant 0.00000000
@FST constant 151.25000000
%FST constant 0.00000177754
@SBIC constant 36.32452638
@AIC constant 36.02194129
@LOGL constant -34.02194129
@NCOEF constant 2.00000000
@NCID constant 2.00000000
@LMAR1 constant 8.5070592D+37
%LMAR1 constant 0.00000000
@LMAR2 constant 8.5070592D+37
%LMAR2 constant 0.00000000
@QSTAT1 constant 3.33333333
%QSTAT1 constant 0.067889155
@QSTAT2 constant 3.38842975
%QSTAT2 constant 0.18374343
@ARCH constant 0.25822990
%ARCH constant 0.61133885
@CSMAX constant 1.26364964
%CSMAX constant 0.0031685821
@CSQMAX constant 0.46590909
%CSQMAX constant 0.050848751
@CHOW constant 53.57142857
%CHOW constant 0.00014913251
@CHOWHET constant 53.57142857
%CHOWHET constant 0.00014913251
@LRHET constant 26.49209701
%LRHET constant 0.00000026462
@WHITEHT constant 3.38983051
%WHITEHT constant 0.18361479
@BPHET constant 1.74908036
%BPHET constant 0.18599239
@SWILK constant 0.86938361
%SWILK constant 0.098324680
BPLIST = list of variables for the Breusch-Pagan heteroscedasticity test.
CALC/NOCALC indicates whether the listed diagnostics (list of output names) should or should not be calculated and stored under @names.
CHOWDATE = starting date of second period for Chow test. The default is to split the sample exactly in half (if the number of observations is odd, the extra observation will be in the second period).
DWPVALUE=APPROX or BOUNDS or EXACT specifies what method will be used for computing the P-value for the Durbin-Watson statistic. The default depends on the current FREQ: APPROX for FREQ N, BOUNDS for other frequencies, including Panel data.
LMLAGS = maximum number of lagged residuals for Breusch-Godfrey LM test of general autocorrelation (AR or MA). The default is zero.
PRINT/NOPRINT indicates whether the diagnostics should be printed. PRINT implies CALC.
PVCALC/NOPVCALC indicates whether p-values should be calculated and stored under %names. PVCALC implies CALC. See Method for the distributions used to compute these P-values in particular cases.
PVPRINT/NOPVPRIN indicates whether p-values should be printed. PVPRINT implies PVCALC, PRINT, and CALC. Using this option will sometimes cause regression output to be printed in one column instead of two, unless SHORTLAB is used. Other things like wide numbers (OPTIONS NWIDTH=, SIGNIF=) may also cause single column output.
QLAGS= maximum number of autocorrelations for Ljung-Box Q-statistics (Portmanteau test of residual autocorrelation). The default is zero.
RESETORD= order of Ramseys RESET test. The default is 2.
SHORTLAB/NOSHORTL indicates whether short or long labels are used when printing all diagnostics.
STAR1= upper bound on p-value for printing at least one star (*), when STARS option is on. The default is .05. There can be up to 5 pairs of (STAR1,STAR2) values, which can apply to different sets of diagnostics. This option only applies to the diagnostics listed for the REGOPT command.
STAR2= upper bound on p-value for printing two stars (**), when STARS option is on. The default is .01 . This option only applies to the diagnostics listed for the REGOPT command.
STARS/NOSTARS indicates whether stars should be printed indicating significance of diagnostics. STARS implies PVCALC, except for regression coefficients (@T).
REGOPT (STARS,LMLAGS=5,QLAGS=5,BPLIST=(C,X,X2)) ALL;
turns on all possible diagnostic output, including VCOV matrix and residual plots.
REGOPT;
restores the default settings.
REGOPT (NOCALC) AUTO;
stops calculation of all the autocorrelation diagnostics (useful for pure cross-sectional datasets).
REGOPT (NOPRINT) RSQ FST;
suppresses printing of the R-squared and F-statistics. This is the same as the old TSP command SUPRES RSQ FST;
REGOPT (STARS,STAR1=.10,STAR2=.05) T ;
REGOPT (,STARS,STAR1=.05,STAR2=.02) AUTO ;
uses one set of significance levels for the t-statistics and another for the autocorrelation diagnostics.
Summary table of diagnostics/OLSQ output (@Name = value, %Name = p-value)
|
Group |
Name |
Description |
|
None |
LHV |
Dependent variable name |
|
|
SMPL |
Current sample |
|
|
NOB |
Number of observations |
|
|
COEF |
Regression coefficients |
|
|
SES |
Standard errors |
|
|
T |
t-statistics |
|
|
VCOV |
Variance-covariance matrix |
|
|
VCOR |
Correlation version of VCOV |
|
|
NCOEF |
Number of coefficients |
|
|
NCID |
Number of identified coefficients (rank of VCOV) |
|
REGOUT |
YMEAN |
Mean of dependent variable |
|
|
SDEV |
Standard deviation of dependent variable |
|
|
SSR |
Sum of squared residuals |
|
|
S2 |
Estimated variance of residuals (SSR/(NOB-NCID)) |
|
|
S |
Standard error of residuals (SQRT(S2)) |
|
|
RSQ |
R-squared (squared correlation between actual and fitted) |
|
|
ARSQ |
Adjusted R-squared (adjusted for number of RHS variables) |
|
AUTO |
DW |
Durbin-Watson statistic |
|
|
DH |
Durbin's h statistic (for single lagged dependent var.) |
|
|
DHALT |
Durbin's h alternative (for any lagged dependent) |
|
|
LMARx |
Breusch-Godfrey LM test for autocorrelation of order x |
|
|
QSTATx |
Ljung-Box Q statistic for autocorrelation of order x |
|
|
WNLAR |
Wald test for nonlinear AR1 restriction vs. Y(-1), X(-1) |
|
|
ARCH |
Test for ARCH(1) residuals |
|
|
RECRES |
Recursive residuals |
|
|
CUSUM |
CUSUM plot |
|
|
CUSUMSQ |
CUSUMSQ plot |
|
|
CSMAX |
CUSUM test statistic |
|
|
CSQMAX |
CUSUMSQ test statistic |
|
|
CHOW |
F-test for stability of coefficients (split sample) |
|
|
CHOWHET |
F-test for stability of coefficients with heteroskedasticity |
|
|
LRHET |
LR test for heteroscedasticity in split sample |
|
HET |
WHITEHT |
White het. test on cross-products of RHS variables |
|
|
BPHET |
Breusch-Pagan het. test on user-supplied list of vars |
|
|
LMHET |
simple LM het. test on squared fitted values |
|
None |
FST |
F-statistic for zero slope coefficients |
|
|
RESETx |
Ramseys RESET test of order x |
|
|
JB |
Jarque-Bera (LM) normality test |
|
|
SWILK |
Shapiro-Wilk normality test |
|
|
AIC |
Akaike Information Criterion |
|
|
SBIC |
Schwarz Bayesian Information Criterion |
|
|
LOGL |
Log of likelihood function |
Method/Notes on specific diagnostics:
DW ignores sample gaps except when there is PANEL data. The DWPVALUE option can be used to choose one of the 3 methods of calculating its P-value. EXACT computes the (T-K) nonzero eigenvalues of the matrix:
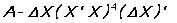
and then uses the Farebrother/Pan method to compute the P-value from the DW and these eigenvalues.
The APPROX method is a small sample adjustment to the asymptotic distribution, using a nonlinear regression fit to the 5% dL (lower bound) table:
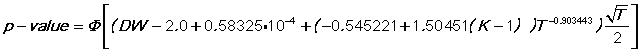
where phi is the cumulative normal. This usually provides a conservative test (i.e. P-value larger than the EXACT method, like the larger number from BOUNDS).
The BOUNDS method calculates the minimum and maximum possible P-values for a given DW, using the minimum and maximum possible sets of eigenvalues for K and T, stored as %DWL and %DWU. See Bhargava et al (1982) for more details on bounds. DW is not computed for OLSQ with explicit lagged dependent variable(s), since it is biased; DH and/or DHALT are computed instead.
The optional AUTO and HET diagnostics are not calculated for regressions with weights, instruments, or perfect fits; nor when there are any gaps in the SMPL (to simplify the processing of lags). Note that some of the later diagnostics grouped under AUTO are not strictly for autocorrelation but for heteroskedasticity or structural stability in datasets with a natural time ordering.
DH is not calculated when it involves taking the square root of a negative value. DHALT can be used in all cases (it uses the same regression as LMAR1).
LMARx prints a series of test statistics if LMLAGS is greater than 1. The sample size is adjusted downwards with each test, and the reported statistic is (p+k-1)*F, asymptotically distributed as chi-squared(p), where p is the number of lags. QSTATx also prints a series of test statistics (using QLAGS).
WNLAR is a Wald test for AR(1) residuals versus mis-specified dynamics (left out lagged dependent and independent variables). If the original equation was Y = A + XB , the regression
Y = A2 + XB + RHO*Y(-1) + D*X(-1)
is run, and the restriction D = -B*RHO is tested. This is asymptotically distributed as chi-squared with degrees of freedom equal to the number of non-singular coefficients on the lagged Xs.
ADF is no longer computed here. See the COINT command.
ARCH is a regression of the squared residual on the lagged squared residual.
RECRES are recursive residuals, calculated using a Kalman Filter (see the KALMAN command). You can display CUSUM and CUSUMQ plots by turning on the PLOTS option. RECRES can also be used for the Von-Neumann ratio test for autocorrelation.
CHOW is an F-test for parameter stability. The default is to split the sample into equal halves, but the CHOWDATE option can be used to choose an unequal split. If there are insufficient degrees of freedom in one of the halves, the test is still valid, but it is usually not very powerful. The CHOWHET test is robust to simple heteroskedasticity and is the MAC2 test from Thursby (1992).
LRHET is a likelihood ratio test for heteroscedasticity between the two periods in the same sample division as the Chow test. Note that the Chow test does not have the assumed F distribution under heteroscedasticity.
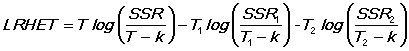
WHITEHT is a regression of the squared residual on cross-products of the RHS variables. If the model is
Y = B0 + B1*X1 + B2*X2
and the residuals are E , the regression
E*E = A0 + A1*X1 + A2*X2 + A3*X1*X1 + A4*X1*X2 + A5*X2*X2
is calculated (if there are sufficient degrees of freedom).
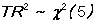
for this example.
BPHET is the same as WHITEHT, except the user specifies a presumably more general list of variables in the E*E regression with the BPLIST option. Note that the ARCH command with the GT option can also be used to estimate such general heteroskedastic regression models.
LMHET is the same as WHITEHT and BPHET, where the squared residuals are regressed on a constant term and the squared fitted values.
RESET is Ramseys RESET test, where the residuals are regressed on the original right hand side variables and powers of the fitted values. The default order (2) is basically a check for missing quadratic terms and interactions for the right hand side variables. It may also be significant if a quadratic functional form happens to fit outliers in the data.
JB is a powerful joint Lagrange Multiplier test of the residuals' skewness and kurtosis. It is asymptotically distributed as a chi-squared with two degrees of freedom under the null of normality. Small sample critical values are:
|
#obs |
20 |
30 |
40 |
50 |
75 |
100 |
125 |
150 |
200 |
250 |
300 |
400 |
500 |
800 |
inf |
|
5% |
3.26 |
3.71 |
3.99 |
4.26 |
4.27 |
4.29 |
4.34 |
4.39 |
4.43 |
4.51 |
4.60 |
4.74 |
4.82 |
5.46 |
5.99 |
|
10% |
2.13 |
2.49 |
2.70 |
2.90 |
3.09 |
3.14 |
3.31 |
3.43 |
3.48 |
3.54 |
3.68 |
3.76 |
3.91 |
4.32 |
4.61 |
SWILK is a normality test based on normal order statistics, which has good power in small samples. Since it involves sorting the residuals, it may be quite slow in large samples. The test and its P-value are computed using Royston(1995), with code from Statlib.
AIC (Akaike Information Criterion) and/or SBIC (Schwarz Bayesian Information Criterion) can be minimized to select regressors in a model, such as choosing the length of a distributed lag. SBIC has optimal properties, see Geweke (1981). In general, these can be defined as
@AIC =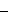 
@LOGL + @NCID*2
@SBIC = 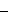@LOGL + @NCID*LOG(@NOB)/2
OLSQ stores normalized versions of these, dividing each by @NOB .
LOGL will include the sum of log weights if the OLSQ (WTYPE=HET,WEIGHT=x) option is used. The alternative is the default WTYPE=REPEAT.
Distributions used for P-values:
Note: in all cases, k is the number of identified coefficients in the model, including the intercept.
|
Test Statistic |
Null |
Alternative |
Distribution |
Degrees of |
|
DW |
No autocorrelation |
Positive autocorrelation (usually) |
ratio of Qform |
-- |
|
DH |
No autocorrelation |
-- |
Normal |
-- |
|
DHALT |
No autocorrelation |
-- |
Normal |
-- |
|
LMARx |
No autocorrelation |
Autocorrelation of order x |
Chi-squared |
p+k |
|
QSTATx |
No autocorrelation |
Autocorrelation of order x |
Chi-squared |
p ? |
|
WNLAR |
AR(1) disturbance |
Other dynamics |
Chi-squared |
# rhs vars |
|
ARCH |
Homoskedasticity |
ARCH(1) disturbance |
Chi-squared |
1 |
|
CSMAX |
Stable parameters |
Parameters change |
Durbin (1971) |
-- |
|
CSQMAX |
Stable parameters |
Parameters change |
Durbin (1969) |
-- |
|
CHOW |
Stable parameters |
Parameters differ between two periods |
F |
(k, nob-2k) usually |
|
CHOWHET |
Stable parameters; variances differ |
Parameters and variances differ between two periods |
F |
(k, nob-2k) usually |
|
LRHET |
Homoskedasticity |
Two variances for split sample |
Chi-squared |
1 |
|
LMHET |
Homoskedasticity |
Heteroskedasticity related to @FIT**2 |
Chi-squared |
1 |
|
WHITEHT |
Homoskedasticity |
X-related Heteroskedasticity |
Chi-squared |
((k+1)k) / 2) - 1 |
|
BPHET |
Homoskedasticity |
Heteroskedasticity related to BPLIST |
Chi-squared |
#vars in BPLIST - 1 |
|
FST |
Y= constant |
Specified regression model |
F |
(k, nob-k) |
|
JB |
Normal disturbances |
Non-normal |
Chi-squared |
2 |
|
SWILK |
Normal disturbances |
Non-normal |
Shapiro-Wilk |
-- |
|
RESETx |
No omitted power terms |
Higher order terms in Xs needed |
Chi-squared |
RESETORD |
|
T |
Slope coefficient =0 |
Slope coefficient not zero |
T (OLS, IV) |
nob-k |
Bhargava, A., L. Franzini, and W. Narendanathan, Serial Correlation and the Fixed Effects Model, Review of Economic Studies XLIX, 1982, pp.533-549.
Brown, R. L., Durbin, J., and Evans, J. M., "Techniques for Testing the Constancy of Regression Relationships Over Time," Journal of the Royal Statistical Society - Series B, 1975, pp. 149-192.
Durbin, J., "Tests for Serial Correlation in Regression Analysis Based on the Periodogram of Least Squares Residuals," Biometrika, 1969.
Durbin, J., "Boundary-crossing probabilities for the Brownian motion and Poisson processes and techniques for computing the power of the Kolmogorov-Smirnov test," Journal of Applied Probability, 8, 1971, pp. 431-453.
Durbin, J., and Watson, G. S. "Testing for Serial Correlation in Least Squares Regression," Biometrika, 1951, pp.160-165.
Farebrother, R. W., "Algorithm AS 153 (AS R52)", Applied Statistics 33, 1984, pp.363-366. Code posted on StatLib, with corrections.
Harvey, Andrew, The Econometric Analysis of Time Series, 2nd ed., 1990, MIT Press.
Geweke, John F., and Richard Meese, "Estimating Regression Models of Finite but Unknown Order," International Economic Review 22, 1981, pp. 55-70.
Jarque, Carlos M., and Bera, Anil K., "A Test for Normality of Observations and Regression Residuals," International Statistical Review 55, 1987, pp. 163-172.
Jayatissa, W. A., "Tests of Equality Between Sets of Coefficients in Linear Regressions when Disturbance Variances are Unequal," Econometrica 45, July 1977, pp. 1291-1292.
Maddala, G. S., Introduction to Econometrics, 1988, Macmillan, Chapters 5, 6, 12.
Royston, Patrick, "Algorithm AS R94, ", Applied Statistics 44, 1995.
Savin, N.E., and Kenneth J. White, Testing for Autocorrelation with Missing Observations. Econometrica 46 (1978): 59-67.
Shapiro, S. S.,and M. B. Wilk, "An Analysis of Variance Test for Normality (Complete Samples) ", Biometrika 52, 1965, pp.591-611.
Shapiro, S. S., M. B. Wilk, and H. J. Chen, A Comparative Study of Various Tests of Normality, JASA 63 (1968): 1343-1372.
Thursby, J., Journal of Econometrics, 1992.
Statlib, http://lib.stat.cmu.edu/apstat/