
RANDOM creates pseudo-random variables. It can create random variables which follow the normal, uniform, Poisson, Negative Binomial, Laplace, t, Cauchy, exponential, gamma, or an empirical distribution. The user may specify (optionally) parameters of the distribution.
RANDOM (CAUCHY, DF=scalar, DRAW=series or matrix, EDF=series, EXPON, GAMMA,
GEN=1 or 2, LAMBDA=scalar, LAPLACE, MEAN=scalar or series, NEGBIN,
POISSON, REPLACE, SEEDIN=scalar, SEEDOUT=scalar,
STDEV=scalar or series, T, UNIFORM, VAR=scalar or series,
VCOV=<variance matrix>, VMEAN=<mean vector>)
series or matrix or <list of series> ;
Usage
RANDOM with no options causes a normal random variable with mean zero and variance one to be generated and stored as a series (under control of the current SMPL). If you want a non-standardized random variable, include the MEAN and STDEV options.
Other options cause the random variable generated to follow the Poisson, negative binomial, uniform, t, Cauchy, exponential, gamma, Laplace (double exponential), or general empirical distributions. See the Examples Section to learn how to obtain random variables from other distributions.
TSP "randomizes" the seed to start every run based on the current time, so you need to specify a fixed seed if you want to reproduce results from run to run. To change the starting seed for any given run or to save it for future use, use the SEEDIN and SEEDOUT options.
If multivariate normal random deviates are desired, the VCOV option is required. The dimension of this (symmetric or diagonal) matrix is the number of series to create. If only one argument is supplied before the semicolon, the series are stored in a matrix with this name. The VMEAN option should be used if a non-zero mean vector is desired.
To create a random variable from an empirical distribution function, a series (usually a set of residuals) generated by the distribution function must be supplied. This feature is useful for computing bootstrap standard errors. A set of residuals generated by the model is used as input to the DRAW option and a new series with the same distribution as the old one is obtained by drawing observations from a discrete distribution with probability mass equal to one divided by the number of observations placed on each observed value of the residuals. This new sample of residuals may then be used in further computations to obtain estimates of functions of these random variables. To draw without replacement, use the NOREPLACE option.
Method
The method used by RANDOM is the multiplicative congruential method. The new uniform generator (GEN=2) has period 2**319, and is a combination of 2 multiple recursive generators with 8 seeds. See L'Ecuyer (1999), generator MRG32k5a. The old uniform generator (GEN=1) has period 2**31-1 and multiplier 41358; this choice is described in L'Ecuyer(1990) (it has optimal "randomness" in its class). Both are implemented in integer math for speed, and to insure a full period (no repeats in 2**31 draws).
The multiplicative congruential method produces random numbers which are uniform on the (0,1) interval. Normal and Poisson random variables are created from uniform random variables with ACM Algorithms #488 and #369, respectively. Gamma random variables use ACM Algorithm #599. Negative binomial random variables are computed by drawing Gamma random variables to determine Y, and then drawing Poisson random variables with mean Y. All other random variables are derived from the uniform random variables using the inverse distribution function, which usually involves an asymptotic expansion (see the CDF references).
CAUCHY/NOCAUCHY specifies that the random number generated is
to follow the Cauchy distribution:
DF = the degrees of freedom for student's t distribution (see the t option).
DRAW = the name of a series which will be sampled with probability one divided by the number of observations to generate the random numbers. This series does not have to be sorted in any order. If DRAW= a matrix, a multivariate set of random numbers is drawn. The number of random variables is equal to the number of columns in the matrix. Note that the matrix from which you are drawing does not have to have the number of rows equal to the number of observations. This is very useful for simulation or bootstrap standard errors.
EDF = Empirical Distribution Function. Same thing as DRAW= .
EXPON/NOEXPON specifies that the random number generated is to follow the exponential distribution:
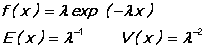
Use the LAMBDA= option to specify the parameter lambda.
GAMMA/NOGAMMA specifies that the random number generated is to follow the gamma distribution:
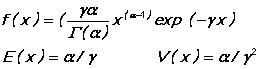
Use the MEAN= and STDEV= options to specify the parameters, which must be non-negative.
GENERATOR = 1 or 2. Type of uniform random number generator. Use GEN=1 to reproduce results from older versions of TSP (to 4.4); this generator has period equal to 2**31 - 1. The new (default) generator has period 2**319.
LAMBDA = the exponential or double exponential parameter. (See the EXPON and LAPLACE options).
LAPLACE/NOLAPLACE specifies that the random number generated is to follow the Laplace (double exponential) distribution:
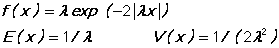
MEAN = the expected value of the random variable or a series containing expected values. Applies only to the normal, gamma, Poisson, and negative binomial random variables. The default value is one (which you will probably wish to override for the gamma and negative binomial distributions). When a series is supplied, each random number drawn will come from a distribution with a different mean.
NEGBIN/NONEGBIN specifies that the random number generated is to follow the negative binomial(N,p) distribution, which is excess waiting time to obtain N successes (the number of trials minus N) with success probability p for each trial. N does not have to be an integer. For this model, the mean and variance of the data are given by
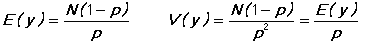
An alternative widely used specification is the following:

The two specifications are equivalent and imply the following identities:

Use the MEAN= and STDEV= options to specify the parameters. The MEAN must be non-negative, and STDEV must be larger than or equal to the square root of the mean.
POISSON/NOPOISSON specifies that the random number generated is to follow the Poisson distribution:

This distribution has one parameter, alpha, which is both the expected value and the variance. Supply this parameter using the MEAN= option. It must be a non-negative number.
REPLACE/NOREPLACE specifies that DRAWing from the empirical distribution function is to be done with replacement (the default) or no replacement.
SEEDIN = value of random seed to start random generator (replaces the current value of the random seed). This must be an integer in the range [1,2.1 billion] (otherwise it is moved into this range). Note that scalar values are stored in double precision, which allows for 16 significant digits, so don't make the seed too large if you are trying to reproduce results. When used with the new default uniform generator, all 8 seeds are set to the SEEDIN value.
SEEDOUT = random seed of the random generator (the current random seed, before any random variables are created by this command). To print the seed, use OPTIONS NWIDTH=20; to provide enough digits. SEEDOUT is not useful with the new uniform generator, because it uses 8 seeds.
STDEV = the standard deviation of the random variable or a series containing standard deviations. This option applies only to normal, gamma, and negative binomial random variables. The default value is one. When a series is supplied, each random number drawn will come from a distribution with a different standard deviation.
T/NOT specifies that the random number generated is to follow student's t distribution with degrees of freedom given by the DF= option.
UNIFORM/NOUNIFORM specifies that the random number generated is to follow the uniform distribution between zero and one.
VAR= the variance of the random variable or a series containing variances. This option applies only to normal, gamma, and negative binomial random variables. The default value is one. When a series is supplied, each random number drawn will come from a distribution with a different variance.
VCOV = (symmetric) variance-covariance matrix for multivariate normal random variables. You can also supply the (triangular) square root of this matrix, which saves a step.
VMEAN = mean vector for multivariate normal random variables (the default is a vector of zeroes).
These examples each generate a thousand random numbers and store them under the series name given.
SMPL 1 1000 ;
RANDOM STDNORM ;
RANDOM (UNIFORM) FLAT ;
FLATAB = FLAT*(B-A) + A ; ? UNIFORM ON THE INTERVAL (A,B).
CDF (CHISQ,DF=3,INV) FLAT CHI3; ? Chi-square(3)
T1EV = -LOG(-LOG(FLAT)); ? Derive Type I Extreme Value from uniform
RANDOM (CAUCHY) FAT ;
RANDOM (EXPON,LAMBDA=2) Z ;
RANDOM (LAPLACE, LAMBDA=0.5) DE ;
RANDOM (T,DF=5) FATAIL ;
RANDOM (GAMMA,MEAN=10,STDEV=2) GAMMA10 ;
RANDOM (NEGBIN,MEAN=10,STDEV=5) NEGBIN10 ;
RANDOM (MEAN=10,STDEV=3.1623) NORM10 ;
RANDOM (MEAN=10,POISSON) POISS10 ;
The last two examples produce random numbers with the same mean and variance, but different distributions. A normal variable with mean 10 and standard deviation 3.1623 could also have been generated by the following:
NORM10 = 10 + STDNORM*3.1623 ;
The next example generates a bivariate normal random vector with correlation 0.5:
LOAD (TYPE=SYM,NROW=2) COVMAT ; 1 .5 1 ;
RANDOM (VCOV=COVMAT) NU1 NU2 ;
Now we use the estimated residuals from a regression to generate 10 samples with the same empirical distribution function:
LIST RES RES1-RES10 ;
RANDOM (EDF=@RES) RES ;
When we are done, the list RES consists of ten series which have the same distribution as the original residual series @RES.
Example with inverse distribution functions:
RANDOM (SEED=94298,UNIFORM) U ;
EV = -LOG(-LOG(U)) ; ? Type I Extreme Value
CDF(INV,CHISQ,DF=n) U CHIV ; ? Chi-square (n)
An example using the matrix version of DRAW to draw data from an empirical distribution function in order to investigate the potential rate of convergence of a particular estimator:
? original data set has 100 observations, compute residuals
SMPL 1 100 ;
OLSQ Y C X ;
UNMAKE @COEF A B ;
MMAKE EDF @RES X ;
? estimation using 1000 obs drawn from EDF
SMPL 1 1000 ;
RANDOM (DRAW=EDF) E X ;
Y = A+B*X+E ;
OLSQ Y C X ;
? estimation using 10,000 obs drawn from same EDF
SMPL 1 10000 ;
RANDOM (DRAW=EDF) E X ;
Y = A+B*X+E ;
OLSQ Y C X ;
Draw 5 cards from a deck of 52 without replacement:
SMPL 1 52 ;
TREND OBS; SUITE = 1+INT((OBS-1)/13) ;
TREND (PER=13) NUMBER ;
MMAKE CARDS SUITE NUMBER ;
SMPL 1 5 ;
RANDOM (DRAW=CARDS,NOREPL) SUITE NUMBER ;
Permute a series of residuals:
SMPL 1 100 ;
OLSQ Y C X1 X2 ;
RANDOM (DRAW=@RES,NOREPL) U ;
Verify that the new uniform generator is properly implemented (check sum of first 10,000,000 r.v.s for seed 12345):
OPTIONS DOUBLE MEMORY=5;
SMPL 1,100000;
RANDOM(GEN=2,SEEDIN=12345);
SET TOTAL=0;
DO I=1,100;
RANDOM(UNIFORM) X;
MAT TOTAL = TOTAL + SUM(X);
ENDDO;
SET CORRECT = 5000494.15;
PRINT TOTAL, CORRECT;
Efron, Bradley, "Bootstrap Methods: Another Look at the Jackknife," Annals of Statistics 7 (1979), pp. 1-26.
Efron, Bradley, The Bootstrap, the Jackknife and Other Resampling Plans, Philadelphia: SIAM, 1982.
Efron, Bradley, and G. Gong, "A Leisurely Look at the Bootstrap, Jackknife, and Cross-validation," American Statistican, February 1983, 37(1), pp. 36-48.
Fishman, George S., and Louis R. Moore, A Statistical Evaluation of Multiplicative Congruential Random Number Generators with Modulus 231-1, JASA 77 (1982), pp. 129 136.
L'Ecuyer, Pierre, "Good Parameter Sets for Combined Multiple Recursive Random Number Generators," Operations Research 47, 1999. http://www.iro.umontreal.ca/~lecuyer/papers.html
L'Ecuyer, Pierre, "Random Numbers for Simulation," Communications of the ACM, October 1990, pp. 85-97.
Schaffer, Henry E., Algorithm #369, Collected Algorithms from ACM Volume II, ACM, New York, 1980..