BJEST

Options     Examples     References

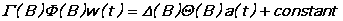
BJEST estimates the parameters of an ARIMA (AutoRegressive Integrated Moving Average) univariate time series model by the method of conditional or exact maximum likelihood. The technical details of the method used are described in Box and Jenkins, Chapter 7. TSP uses the notation of Box and Jenkins to describe the time series model.

BJEST (CONSTANT, CUMPLOT, EXACTML, NAR=<number of AR parameters>,

               NBACK=<number of back-forecasted residuals>, NDIFF=<degree of differencing>,

               NLAG=<number of autocorrelations>, NMA=<number of MA parameters>,

               NSAR=<number of seasonal AR params>,

               NSDIFF=<degree of seasonal differencing>,

               NSMA=<number of seasonal MA parameters>, NSPAN=<span of seasonal>,

               PLOT, START, nonlinear options)

               [<series name>] [START <parameter name> <parameter value> ......]

               [FIX <parameter name> <parameter value> ......] [ZERO <parameter names> .....]

               [ZFIX <parameter names> .....] ;

Usage

To estimate an ARIMA model, use the BJEST command followed by the options you want in parentheses and then the name of the series and specification of the starting values, if you want to override the default starting values.

The general form of the model which is estimated is the following:

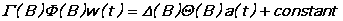
w(t) is the input series after ordinary and seasonal differencing, and a(t) is the underlying "white noise" process. B is the "backshift" or lag operator:

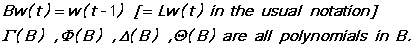
The order of these polynomials is specified by the options NSAR, NAR, NSMA, and NMA respectively. Gamma(B) and Delta(B) are the seasonal AR and MA polynomials and Phi(B) and Theta(B) are the ordinary AR and MA polynomials. All the polynomials are of the form

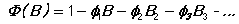
Note that the coefficients all have minus signs in front of them.

The BJEST procedure uses conditional sum of squares estimation to find the best values of the coefficients of these polynomials, consistent with the unobserved variable at being independently identically distributed. The options specify the exact model which is to be estimated and can also be used to control the iteration process.

As with the other iterative estimation techniques in TSP, it is helpful to specify reasonable starting values for the parameters. Unlike the other nonlinear TSP procedures, the starting values for BJEST can be specified directly in the command, not with a PARAM statement, since the parameters have certain fixed predetermined names in the Box-Jenkins notation.

There are several ways to specify starting values in BJEST. The easiest way is to let TSP "guess" reasonable starting values for the parameters. TSP will choose starting values, for the non-seasonal parameters only, based on the autocorrelations of the time series. You can suppress this feature with NOSTART. If no other information is supplied (see below), TSP will use zero as the starting value for all the parameters. In practice, this generally leads to slower convergence of the parameter estimates. You can also supply starting values in an @START vector.

You may also specify the starting values for any or all of the parameters yourself. For a model with more than one or two parameters, it may be difficult to choose starting values, since the individual parameters often do not possess a simple interpretation. However, you may wish to specify the starting values of at least some of the parameters based, perhaps, on previous estimates. In this case any parameters for which no starting value is supplied will be given the default value (TSP's guess if the START option is on, or zero for NOSTART, or the @START value).

User-supplied starting values are given after the name of the series on the command. Follow the series name with the keyword START and then a series of pairs of parameter names and starting values. The names available are:

The lag in parentheses should be an actual number giving the position of the coefficient in the lag polynomial, i.e., AR(1) means the coefficient which multiplies the series lagged once (AR(0) is always unity).

Sometimes it is useful to fix a parameter at a certain value while others are being estimated. This may be done to limit the number of parameters being estimated, or to incorporate prior information about a parameter value, or to isolate an estimation problem which is specific to one or a few parameters. The keyword FIX followed by pairs of parameter names and values can be used to achieve this. FIX and START can be used on the same BJEST command to give starting values to some parameters and hold others fixed. The ZERO keyword is used to override the automatic starting values for some parameter(s) with zero(s). The ZFIX keyword fixes some parameter(s) to zero.

BJEST can also be used to check roots of polynomials for stationarity/invertability, without doing any estimation. Just supply the coefficient values in @START, use NAR=p and/or NMA=q, and do not supply a dependent variable. The PRINT option will print the roots, or the @ARSTAT and @MAINV variables can be used.

Output

The output of BJEST begins with a printout of the starting values, followed by an iteration log with one line per iteration giving the value of the objective function and the convergence criterion. If the PRINT option is on, the convert values of the options and the exact time series process being used are printed. In the iteration log, parameter values and changes are printed for each iteration when PRINT is on.

When convergence of the iterative process has been achieved or the maximum number of iterations reached, a message to that effect is printed, and the final results are displayed. These include the conventional statistics on the model: the standard error of at, the R-squared and F-statistic for the hypothesis that all the parameters are zero. The parameter estimates and their standard errors are shown in the usual regression output.

When the PRINT option is on, If the order of any polynomial is greater than one, its roots and moduli are shown so that you can check that they are outside the unit circle (as is required for stationarity). A table of the autocorrelations and Ljung-Box modified Q-statistics of the residuals is printed after this. If the PRINT option is on, the exact model estimated is again printed in lag notation, along with some summary statistics for the residuals. Then comes a printout of the lagged cross correlations between the differenced series wt and the white noise (residual) series at.

If the PLOT option is on, a time series plot of the residuals (at) is printed. If the CUMPLOT option is on, a normalized cumulative periodogram is also plotted (see the CUMPLOT option above).

The following variables are stored (statistics based on differenced variable if differencing is specified):

Method

The method used by BJEST (for the default method NOEXACTML) to estimate the parameters is essentially the one described by Box and Jenkins in their book. It uses a conventional nonlinear least squares algorithm with numerical derivatives. The major difference between the estimation of time series models and estimation in the traditional (nonlinear least squares) way relates to the use of "back-forecasted" residuals. The likelihood function for the ARIMA model depends on the infinite past sequence of residuals. If we estimate the time series model by simply setting the values of these past residuals to zero, their unconditional expectation, we might seriously misestimate the parameters if the initial disturbance, a0, happens to be very different from zero.

The solution to this problem, suggested by Box and Jenkins, is to invert the representation of the time series process, i.e., write the same process as if the future outcomes were determining the past. Thus it describes the relationships which the time series will, ex post, exhibit. This representation of the backward process constructs back-forecasts of the disturbance series, the at series and then uses these calculated residuals in the likelihood function. By using a reasonable number of these backcasted residuals, the problems introduced by an unusually high positive or negative value for the first disturbance in the time series can be eliminated.

If the process is a pure moving average process, this backcast becomes zero after a fixed number of time periods; consequently, you can set NBACK to a fairly small number in this case.

When the EXACTML option is used, no backcasting is done; the AS 197 algorithm (Melard 1984) is used.

Options

Note that for all the Box-Jenkins procedures (BJIDENT, BJEST, and BJFRCST), TSP remembers the options from the previous Box-Jenkins command (except for nonlinear options), so that you only need to specify the ones you want to change.

CONSTANT/NOCONS specifies whether a constant term is to be included in the model.

CUMPLOT/NOCUMPLO specifies whether a cumulative periodogram of the residuals is to be plotted. The number of computations required for this plot goes up with the square of the number of observations, so that it may be better to forego this option if the number of observations is large.

EXACTML/NOEXACT specifies exact (versus conditional) maximum likelihood estimation. EXACTML is recommended for models with a unit root in the MA polynomial. This option is not yet fully integrated with all the other options; it does not support NSAR>0 or NSMA>0, or automatic computation of starting values (use @START). It also does not (yet) impose invertability on the MA polynomial for NMA>1 .

NAR= the number of autoregressive parameters in the model. The default is zero.

NBACK= the number of back-forecasted residuals to be calculated. The default is 100.

NDIFF= the degree of differencing to be applied to the series. The default is zero.

NLAG= the number of autocorrelations/Q-statistics to calculate. The default is 20.

NMA= the number of moving average parameters to be estimated. The default is zero.

NSAR= the number of seasonal autoregressive parameters to be estimated. The default is zero.

NSDIFF= the degree of seasonal differencing to be applied to the series. The default is zero (no differencing).

NSMA= the number of seasonal moving average parameters to be estimated. The default is zero.

NSPAN= the span (number of periods) of the seasonal cycle, i.e., for quarterly data, NSPAN should be 4. The default is the current frequency (that is, 1 for annual, 4 for quarterly, 12 for monthly).

PLOT/NOPLOT specifies whether the residuals are to be plotted.

START/NOSTART specifies whether the procedure should supply its own starting values for the parameters.

Nonlinear options control iteration and printing. They are explained in the NONLINEAR entry.

Examples

This example estimates a simple ARMA(1,1) model with no seasonal component; no plots are produced of the results.

BJEST (NAR=1,NMA=1,NOPLOT,NOCUMPLO) AR9MA5 ;

This example uses the Nelson (1973) auto sales data; a logarithmic transformation of the series is made before estimation.

GENR LOGAUTO = LOG(AUTOSALE) ;

BJEST (NDIF=1,NSDIFF=1,NMA=2,NSMA=1,NSPAN=12, NBACK=15) LOGAUTO

START THETA(1) 0.12 THETA(2) 0.20 DELTA(1) 0.82 ;

Note that NBACK is specified as 15 since the backcasted residuals fall to exactly zero after NSPAN+NSMA+NMA periods in a pure moving average model.

The next example estimates a third order autoregressive process with one parameter fixed:

BJEST GNP START PHI(2) -0.5 PHI(3) 0.1 FIX PHI(1) 0.9 ;

The model being estimated is

GNP(t) - 0.9*GNP(t-1) - 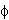2*GNP(t-2) - 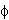3*GNP(t-3) = a(t)

Exact ML estimation:

MMAKE @START .1 .1 .1;

BJEST(NAR=2,NMA=1,NDIFF=1,EXACTML) Y;

References

Box, George P. and Gwilym M. Jenkins, Times Series Analysis: Forecasting and Control, Holden-Day, New York, 1976.

Ljung, G.M., and Box, George P., "On a measure of lack of fit in times series models," Biometrika 66, 1978, pp. 297-303.

Mélard, G., "Algorithm AS 197: A Fast Algorithm for the Exact Likelihood of Autoregressive-moving Average Models," Applied Statistics, 1984, p.104-109. (code available on StatLib)

Nelson, Charles, Applied Times Series Analysis for Managerial Forecasting, Holden-Day, New York, 1973.

Pindyck, Robert S. and Daniel L. Rubinfeld, Econometric Models and Economic Forecasts, McGraw-Hill Book Co., New York, 1976, Chapter 15.

Statlib, http://lib.stat.cmu.edu/apstat/